[Image recognition] Resnet Review

3 분 소요

Alt text

Resnet 논문 리뷰

본 논문리뷰는 논문 구성을 따르고 있지만, 단지 제 생각을 구성에 맞춰서 적은 것이지

실제 논문을 요약하여 적은 것이 아닙니다. 착오 없으시길 바랍니다.

Resnet에 관한 정보

  1. Microsoft Research팀에서 publish한 본 논문을 구현한 모델
  2. ILSVRC(Imagenet Large Scale Visual Recognition Challenge) 우승
  3. COCO 2015 우승
  4. Imagenet detection, imagenet rocalization, COCO detection, COCO segmentation 1st prize
  5. 아직도 많은 사람들이 backbone network로써 사용하는 모델(Detection이나 classification 분야에서)

Introduction

우리가 해결해야 할 문제가 Detection이나 Classification과 같은 문제라고 했을 때

네트워크는 어떻게 설계되어야 좋을까요?

깊게? 얕게? 넓게?

사실 어떤 플랫폼에서 어떤 객체들을 얼마나 깊은 깊이로 등 specific한 정보가

정해지지 않는 한 이 질문은 크게 의미가 없습니다.

이 질문에 대한 답은 여기(링크걸기)에서 같이 고민해보기로 하고

AlexNet의 등장 이후로 일반적으로는 딥러닝 네트워크는 깊어지면 깊어질 수록 성능이 더 좋다고 알려져있습니다.

하지만 Resnet의 등장 이전, 사람들은 깊이 있는 네트워크를 설계하고 싶어도

Gradient vanishing 문제 때문에 레이어를 깊게 쌓아나가는데 한계가 있었죠.

(Overfitting 문제가 아닌가 하고 생각이 든다면 K. He and J. Sun. Convolutional neural networks

at constrained time cost. In CVPR, 2015 를 참조하시면 좋을 듯 합니다.)

아래 그림을 봅시다.

alt text

그림에는 20-Layer와 56-Layer가 비교되어 있는데, 20-Layer보다 56-Layer의 error-rate가 더 높은걸 확인할 수 있는데

이 처럼 network가 조금만 깊어지더라도 오히려 얕은 network보다 성능이 저하되는 문제가 발생하곤 했습니다,

하지만 Resnet은 망을 152층까지 쌓고도 당대 최고의 accuracy를 내는데 성공했고, 그 이후에는 1001층까지 쌓는데도 성공하였습니다.

어떻게 그렇게 깊게 쌓을 수 있었을까요?

Approach - Residual Learning

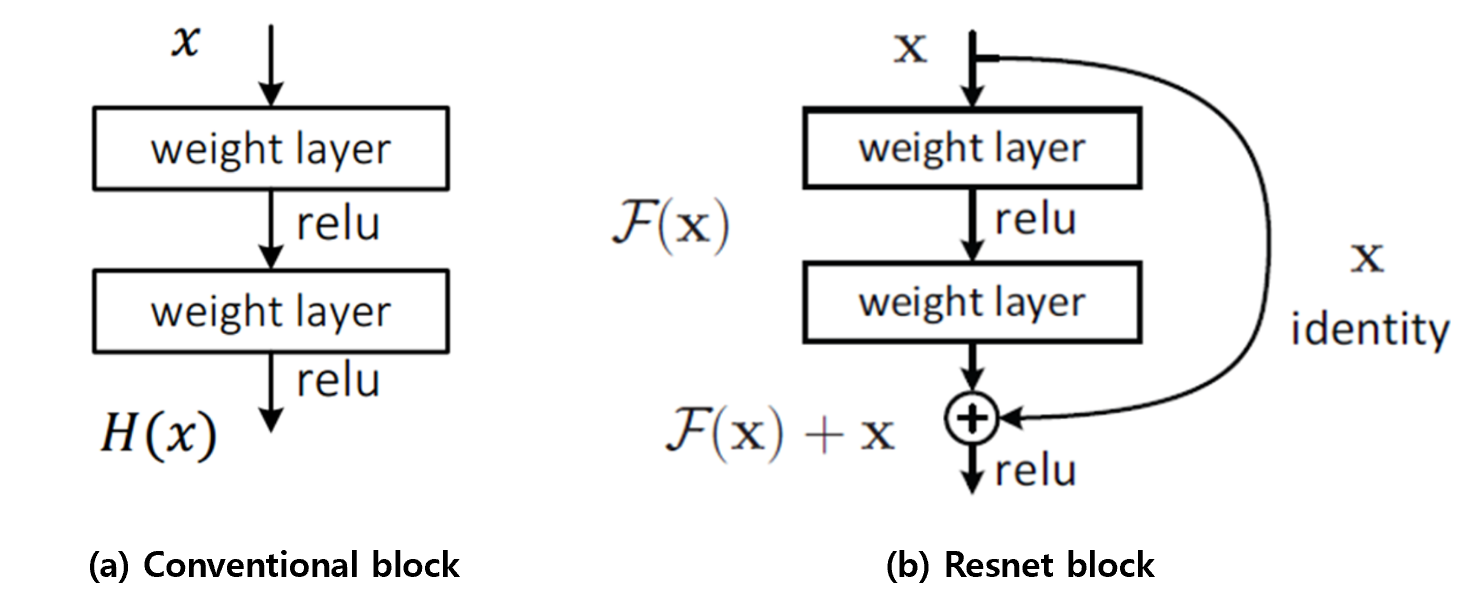
alt text

위 그림에서 (a)와 (b)는 일반적인 plain net block과 resnet에서의 block을 나타내고 있습니다.

이 Resnet block이 Resnet에서의 핵심적인 역할을 하는 block인데

여기에서 나타난 것 처럼 Input X가 weight layer와 RELU를 지난 결과값을 H(x)라고 한다면

(b)의 resnet block은 입력 x와 weight layer 및 RELU를 지난 중간 결과값 F(x)가 더해져 H(x) = x + F(x)로 나타낼 수 있습니다.

(이렇게 Output에 Input인 x를 Skip-connection(Shortcut-connection)을 통해서 F(x)에 바로 더해주는 방식을 identity-mapping이라고 합니다.)

이 때, 이 네트워크는 Detection이나 Classification을 목표로 하고 있으므로

실제로는 학습시에는 조금의 차이가 있을 수 있지만, 만약 Input x가 어떠한 객체로 분류될 Input이었다고 하면

Label값 역시 x와 유사한 값일 것입니다.

따라서, 이 Output이 cost로 바뀌어서 학습될 때를 생각하면 cost는 x - H(x) = -F(x)로 나타낼 수 있고

결국에 우리는 cost가 0이 되는걸 목표로 하고 있으므로 -F(x)는 0이 되는걸 목표로 하게 되는 것입니다.

길게 설명했지만, 결국엔 F(x)는 실제 값과의 차이를 나타낸다고 할 수 있고, 즉 이것이 바로 Residual(나머지) 가 되는 것입니다.

결국 네트워크 이름이 Resnet인 이유도 이 residual을 0으로 만드는 방향으로 나타내는 네트워크라서 ResidualNet->ResNet 이라 불리는 것입니다.

이 Resnet block은 단지 Input이 Output에 더해지기만 할 뿐이라 연산량 측면에서도 거의 변화가 없을 뿐더러

입력을 더해주는 행위가 정보량을 보존해줘서 계속된 전파(Backward)에도 정보량을 유지하며 학습되어서

결과적으로는 Gradient vanishing problem을 해결할 수 있는 것입니다.

추가적으로, Resnet의 후속 논문인 Identity Mappings in Deep Residual Networks에서 주장하는 바에 따르면

Identity mapping 방식이 아닌 일반 방식을 채택했을 때, Input x에 곱해지는 수를 a라고 하면

  • a>1 : Gradient가 vanish될 것
  • a<1 : Gradient가 explode될 것

이라고 주장하며 깊은 네트워크로 갈 때의 identity mapping의 중요성을 강조하고 있습니다.

Approach - Network Architecture

저자는 이 모델에 관한 실험을 진행함으로써 지속적인 현상을 발견했고, 이를 잘 보여주기 위해 plainNet을 만들고 Resnet과 비교하였습니다.

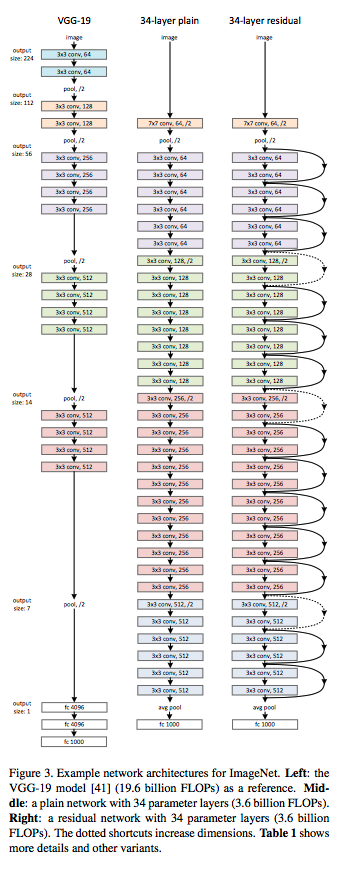
alt text

그림의 설명대로, (a)는 plainnet의 참고 모델인 VGG, (b)는 plainnet, (c)는 plainnet에 shortcut-connection을 추가한 resnet입니다.

(VGG의 설계를 따랐지만 FLOPS는 11.3 Billion으로 VGG-16/19의 1.53/19.6 Billion보다 낮습니다.)

또한 plainNet을 설계할 때에는 아래와 같은 규칙을 따랐습니다.

  1. feature map의 output size가 같은 경우에는 같은 수의 filter를 사용한다.

  2. feature map의 사이즈가 반이 되었을 때에는 layer의 complexity를 유지하기 위해서 filter의 수를 두 배로 한다.

  3. feature map의 사이즈를 줄이기 위해서는 stride를 2로하여 줄인다.

추가적으로 resNet을 설계할 때에는 short-cut 후 F(x)와 더해질 때의 demention을 유지하기 위해서

zero-padding과 1x1 convolution을 사용하였습니다.

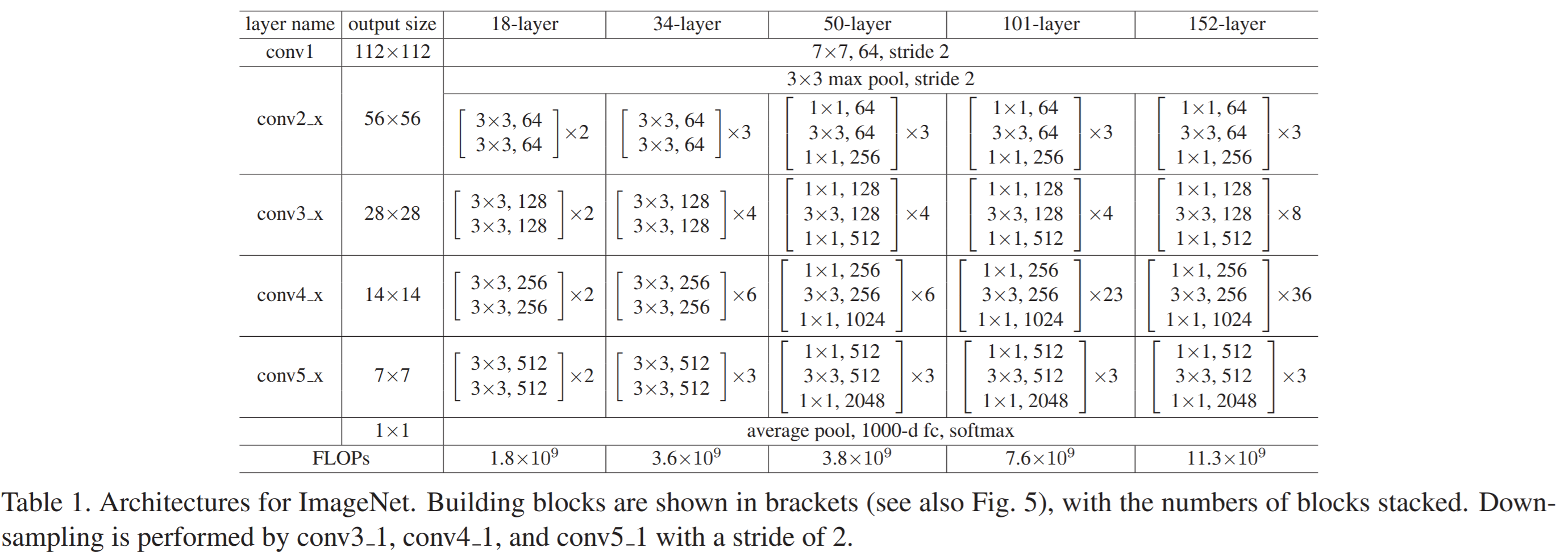
alt text

실제 학습 세팅은 아래와 같습니다.

  1. Input size = (224,224)

  2. Use batch-normalization layer right after conv layer (conv-bn-RELU 순으로 할당)

  3. Optimizer = SGD, weight_decay = 0.0001, momentum = 0.9

  4. Batch-size = 256

  5. Iteration = 600000

  6. Didn’t use dropout

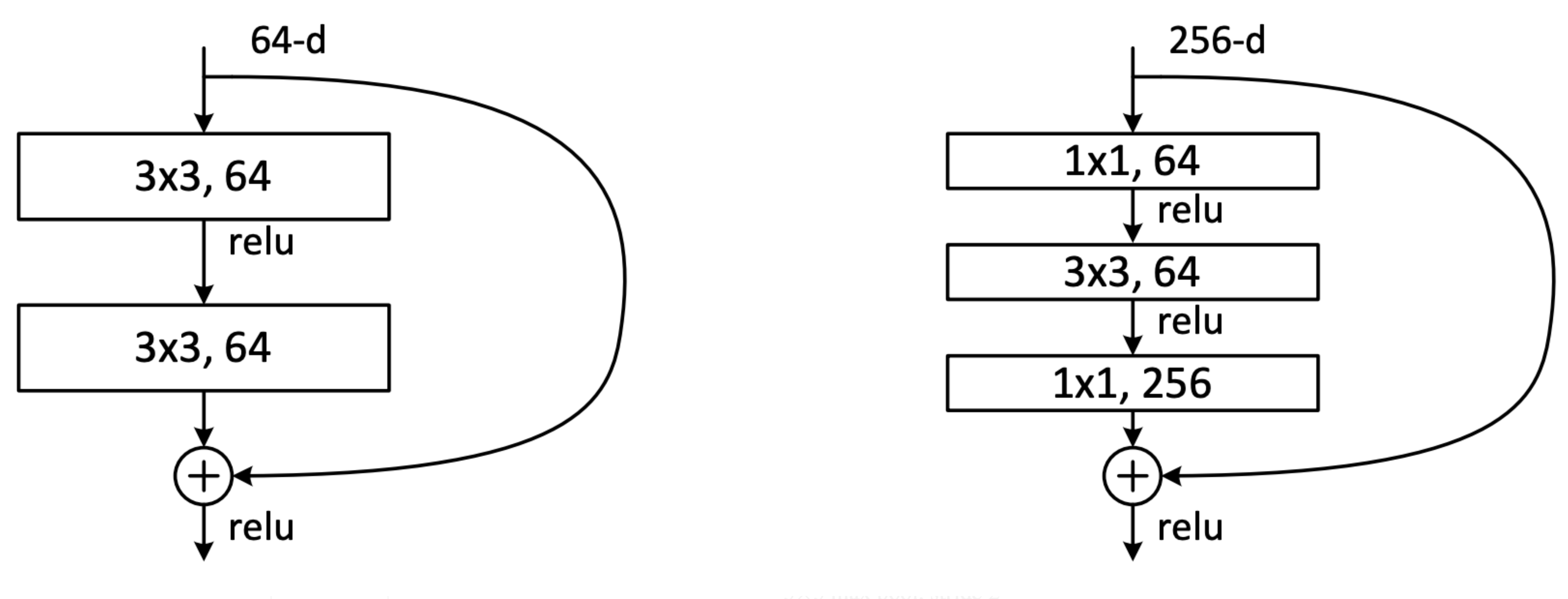
alt text

추가적으로, 저자는 short-cut을 두 가지 형태로 design하였으며

좌측의 원래 모델에 비해서, 우측의 모델을 사용함으로써 정확도는 줄이지 않으면서

1x1 convolution을 통해 파라미터수를 줄일 수 있음을 밝히며 1x1 convolution을 사용한모델을 projection-shortcut으로 명명하였습니다.

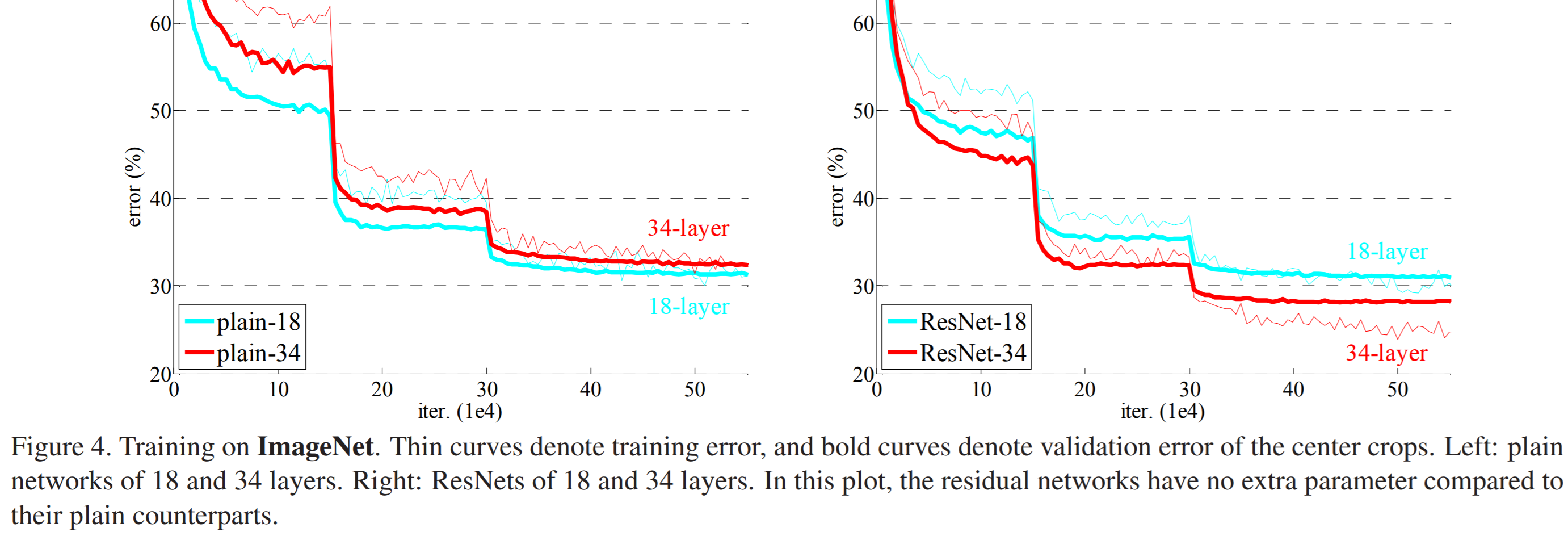
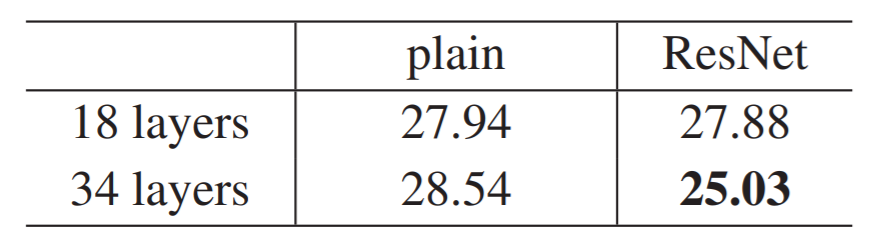
alt text alt text

위의 figure은 일반적인 plainNet은 18-Layer보다 34-Layer가 error가 더 높지만

Resnet의 경우에는 18-Layer보다 34-Layer의 error가 더 낮은 것을 통해

ResNet의 Gradient vanishing 예방이 성공적이라는 것을 짐작할 수 있습니다.

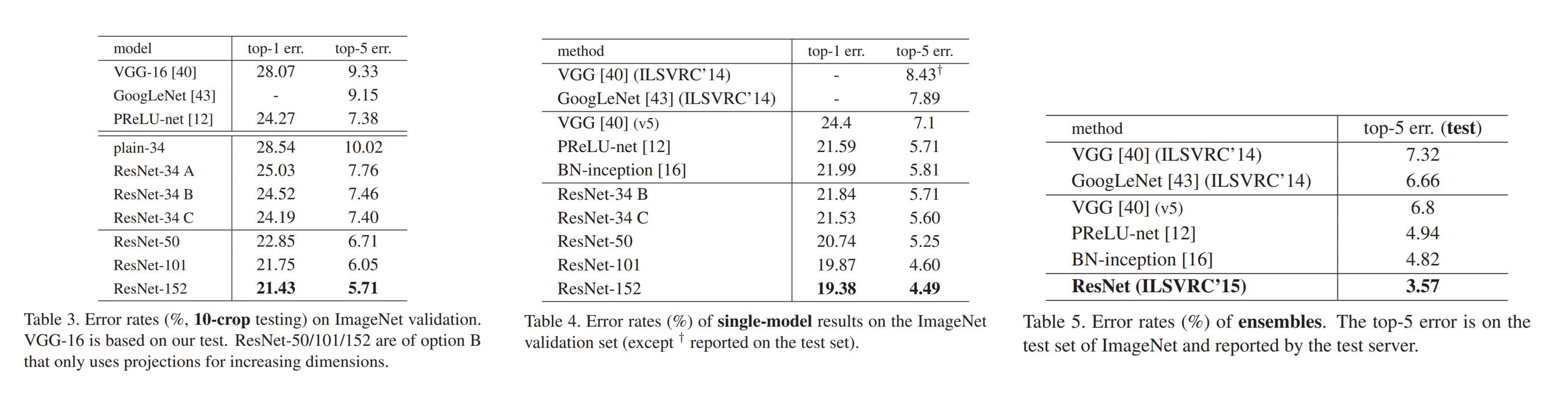
alt text

또한 Table 3에서는 ImageNet dataset에서의 비교를 제시하였는데

ResNet(a)는 demension을 늘리기 위해 identity-mapping을 사용한 모델이고

ResNet(b)는 demension을 늘리기 위해서는 projection-shortcut을, 그 외에는 identity-mapping을

ResNet(c)는 모든 short-cut에 projection-shortcut을 적용한 모델입니다.

결과는 a보다는 b가, b보다는 c가 좀 더 낫지만, 아주 미미한 차이이고 모델의 복잡성 문제로 (c)는 더 이상 언급하지 않겠다고 말합니다.

Table 4와 5에서는 state-of-the-art 모델들만 언급하였는데

Table 4는 single model들을 언급하였고

Table 5는 ensemble 모델들을 언급하였습니다.

결국에는 이 앙상블 기법을 적용한 ResNet은 오류율 3.57%를 달성하게 되고, 결국 2015년 ILSVRC 대회에서 우승을 거머쥐게 됩니다.

마치며

이렇게 ResNet에 대한 리뷰가 끝이 났습니다.

첫 논문 리뷰 포스팅이라 제가 전달하려고 했던 내용들이 잘 전달이 됐을까 모르겠네요.

읽어주셔서 감사합니다.

이만 줄일게요!

댓글남기기

참고