[Mathmatics for machine learning] Analytic Geometry

Mathmatics for machine learning

• 본 포스팅은 Mathmatics for learning을 공부하는 과정에서, 기억해야 할 개념이나 햇갈리는 개념만 모아서 정리한 개인 정리용 포스팅입니다.

1. Norm

• Norm은 vector의 크기를 나타내는 표현 방법.

• $\lVert x \rVert$와 같이 표현.

• 일반적으로 생각할 때, 각 차원에 맞는 Norm은 $\sum_{i=1}^{n}(

  x_{i}

  ^{p})^{\sqrt{1}{p}}$.

• 아래의 3가지 성질을 가진다.

• 

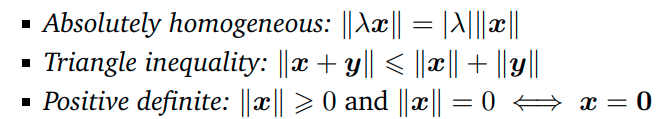
• Loss로는 보통 MAE (L1 Norm), MSE (L2 Norm)을 많이 사용한다.

• L1 Norm은 수렴 속도가 상대적으로 느린데, 특이치에 강하고

• L2 Norm은 수렴 속도가 상대적으로 빠른데, 특이치에 약하다. (특이치도 제곱해버리니까)

2. Inner product

• 두 Vector 간의 product를 통해서 scalar value로 매핑시키는 것을 의미. (즉, $R^n$으로 매핑)

• 주로 Scalar product 및 dot product가 있다.

• Bilinear mapping (Argument를 2개 가지는 linear mapping)에서 아래의 성질을 갖는다.

• 

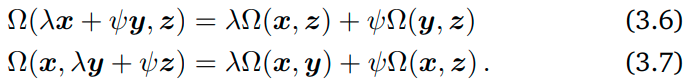
  • 이건 당연히 linear mapping의 성질으로부터 나온 성질들. 굳이 외울 필요 없이 Linear mapping의 성질만 잘 알면 유추 가능.

  • 

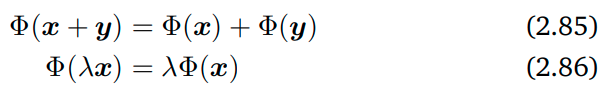
  • 잠깐!! 아래의 개념을 기억하나??

  • 

  • 

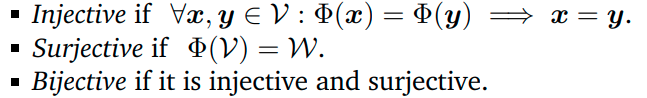
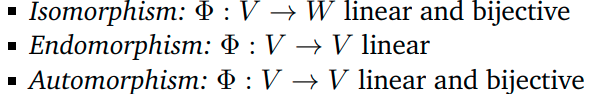
  • 2.1. Symmetric Positive definite matrices

    • Symmetric positive definite matrices란 x, y의 inner product를 아래의 식 (3.10)을 통해서 나타낼 때, 연산 스칼라 값이 양수이고, A 행렬이 대칭 행렬 (Symmetric matrix)일 때의 A를 의미한다.

    • 

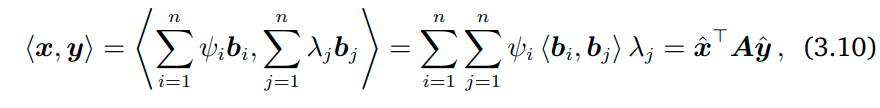
    • 이 때 $\hat{x}$, $\hat{y}$ 은 각각 특정 행 벡터 및 열 벡터를 의미하며, 그 차원은 A의 1-axis의 차원과 같다.

    • 즉, $\hat{x}$ 은 1xn, A는 nxn, $\hat{y}$ 은 nx1 이므로, 최종 연산 값은 scalar 값이 나오게 되며, 해당 scalar 값이 양수이고 A가 Symmetric해야 symmetric positive definite matrices가 되는 것이다.

    • 근데 이게 왜 중요하냐?

      • A가 Symmetric positive definite matrices 일 때, A의 Null space (A와 inner product해서 zero로 projection 시키는 벡터 공간)는 오로지 0이 될 수 밖에 없다. (최종 scalar 값이 0 이상이니까!)

      • 실수 차원에서 Standard basis간의 내적이 0보다 클 때, A의 대각 성분이 항상 0보다 크기 때문.

      • 이라고 책에 나와있는데.. 사실 첫 번째 성질은 어느정도 느낌이 오는데, 두 번째 성질은 느낌이 잘 안온다.. Chapter 12에서 kernel을 배울 때 좀 더 자세히 다룬다고 하니, 그 때 보완해보자.

3. Lengths and distances

• Norm이 vector의 length 및 distance를 나타낸다는 것.

• 설명할 건 딱히 없음. 아는 성질

4. Angles and orthogonality

• Angles

  • $\overrightarrow{x}$ 및 $\overrightarrow{y}$ 간의 내적이 $\lVert x \rVert$ $\lVert y \rVert$ cos($\theta$) 이기 때문에, 내적을 두 벡터의 크기의 곱으로 나눈 후 arccos을 취하는 방식으로 angle을 도출 가능하다는 것.

• Orthogonality

  • 직교하는 두 벡터는 inner product 값이 0이 된다는 것.

• Orthogonormal matrix

  • Matrix의 각 column이 서로 orthogonal하고 크기가 1일 때 orthogonormal하다고 부른다.

  • 이 성질을 만족하는 행렬을 orthogonal matrix라고 부른다.

  • 이 행렬의 전치 행렬은 이 행렬의 역행렬과 같다.

  • 이 행렬은 vector에 곱해져도 그 크기를 바꾸지 않는다.

  • 또한 두 벡터에 모두 orthogonal한 matrix를 곱했을 때 두 벡터 사이의 각도 바뀌지 않는다.

  • 따라서 Rotation과 같은 linear transformation을 할 때, orthogonal matrix가 사용된다.