[Linear algebra] Linear transformation and matrix
Linear algebra 2강
본 포스팅은 김영길 교수님의 유튜브 강의를 보고 개인적인 공부 목적으로 적은 것 임을 밝힙니다. 문제가 될 시 삭제하겠습니다.
목차
- Vector space
- Linear transformation and matrix
- System of linear equations
- Determinant
- Diagonalization
- Inner product space
2.1 Linear transformation
T: V -> W (여기서 V는 Domain(정의역), W는 Codomain(공역)) T는 Linear transformation을 뜻하고
T가 V -> W의 Linear transformation이 되려면
$T(x + y) = T(x) + T(y)$ - (Additivity)
$T(cx) = cT(x)$ - (homogeneity)
를 모든 x,y in v, c in F에서 성립해야한다. 두 조건을 만족시키는 것을 Super position principle이 성립한다. 고 표현한다.
즉, addition 및 scalar multiplication을 preserve하는 것을 Linear map(= Linear transformation) 이라고 한다.
Properties of Lienar map
- $T(0) = 0$ (Zero vector 의 output은 Zero-vector이다) (즉 해당되는 공간의 벡터는 항등원 및 역원이 존재해야하고, 그렇게 되면 반드시 원점을 지나게 되므로, 당연히 Zero-vector의 Output은 Zero-vector가 된다.)
즉, 아래 그림은 Linear하지 않다.
-
$T(cx + y) = cT(x) + T(y)$
-
$T(x - y) = T(x) - T(y)$
-
$T(\sum_{i=1}^{n} a_i*x_i)$ = $(\sum_{i=1}^{n} a_i * T(x_i)$) -> 즉 스칼라곱을 미리하고 Linear transformation을 하나, 나중에 하나 같다는 것이다.
Ex 1. $T: R^2 \to R^2$
$(a1, a2) \to (2a1 + a2, a1)$이 LT인가?
2번 성질을 이용해서 풀어봤을 때 성공적이므로 맞다. (LT를 하기 전에 연산을 하던, LT를 한 후에 연산을 하던 같다는 것이다. 위 식에서 T는 연산, -> 는 LT를 뜻한다.)
Ex 2. $T: R^2 \to R^2$
위 그림에서 벡터가 세타만큼 회전하는게 LT인지의 증명은 Additivity 및 homogeneity를 증명하면 된다.
Reflection
$T: R^2 \to R^2$ 일 때 $(a1, a2) \to (a1, -a2)$는 LT인가?
역시 Additivity 및 homogeneity를 증명하면 LT라는 걸 알 수 있다.
Projection
이렇게 벡터의 정사영을 내리는 것도 LT이다.
증명은, 어떤 두 벡터의 합의 정사영과 두 벡터 각각의 정사영의 합이 같으면 Additivity가 성립하고
마찬가지로, 한 벡터의 곱의 정사영과, 그 벡터의 정사영의 곱이 같으면 homogeneity가 성립한다는 것을 알 수 있다.
미분, 및 정적분도 LT이다. (부정적분은 상수 C가 튀어나와버리니까 LT가 아니게되어 버릴 수 있다.)
Linear transformation some cases
- Identity transformation
- $ V \to V$ 공간에서 $x \to x$
- Zero transformation
- $V \to W$ 공간에서 $x \to 0$
Nullspace
-
$V \to W$ LT할 때 W에서 0가 되는 V내 벡터들의 집합을 Nullspace라고 한다.
-
Identity transformation에서는 $x \to x$ 여야 하므로, Nullspace가 되는 집합은 $x = 0$으로만 구성된다.
-
Zero transformation에서는 $x \to 0$ 이어야 하므로, Nullspace가 되는 집합은 V 내 속한 벡터 전체이다.
image / preimage / Range
-
image : $X \to Y$로 LT했을 때 $x \to y$가 된다고 하면, y가 image가 된다.
-
pre-image : $X \to Y$로 LT했을 때 $x \to y$가 된다고 하면, x가 pre-image가 된다.
-
Range : 치역의 부분집합을 의미한다. 즉 image들의 집합을 의미한다고 생각하면 될 듯.
Ex 8.
- $I: V \to V$ 에서, $x \to x$일 때
$N(I) = {0}$이고, $R(I)$는 그 자체가 된다.
EX 9.
- $T0 : V \to V$ 에서, $x \to 0$ 일 때
$N(T0) = V, R(T0) = {0}$가 된다. 설명은 필요없겠지?
Ex 9-1
- T: $R^3 \to R^2$
$(a1, a2, a3) \to (a1 - a2, 2a3)$ 일 때 Nullspace는 a1 = a2이고, a3=0 일 때의 집합을 의미하므로
Span(1,1,0)이 T의 Null space가 된다.
여기서 Range는 전체 집합이 된다. 왜냐하면 a1, a2, a3의 조절로 모든 R^2를 만들어낼 수 있으므로
Thm 2.2
$T: P2(R) \to M_2*2(R)$ 이 선형적일 때,
V의 basis의 집합이 b일 때, $R(T) = Span(T(B))$를 증명.
증명을 위해서는 서로 속한다는 걸 증명해야 함.
$Span(T(b))$ in $R(T)$ 증명
basis의 image는 $R(T)$ 내에 포함되어 있다. 이는 W의 Subspace이므로 그 부분집합의 (basis의) span 또한 반드시 포함해야하므로 증명된다.
## Ex. 10
- $T: P_2(R) \to M_22(R)$ Linear 할 때, f(x) = a2x^2 + a1*x + a0 \to [f(1) - f(2) 0 ] [ 0 f(0) ] basis = {1, x, x^2} 일 때 P_2(R).
$T(f(X)) = T(1)$ = a2=0, a2=0 이라는 뜻.
Nullity and Rank
-
Nullity = Nullspace의 dimension
-
Rank = Range의 dimension
one-to-one(단사함수), onto(전사함수)
-
One-to-one mapping => $x != y \to T(x) != T(y)$ (정의역이 서로 다를 때, 치역 역시 서로 다른 것)
-
Onto mapping T(V) = W (치역과 공역이 같을 때)
Ex. 11
-
$T: P_2(R) \to P_3(R)$
-
T(f(x)) = 2/prime{f}(x) + \integral{0}^{x} 3f(t)dt
-
일 때 rank(T), nullity(T), one-to-one, onto를 구하라
-
즉 2차식 -> 3차식으로 갈 때 저 4가지를 구하라~ 이 문제이다.
-
$R(T) = Span({T(1), T(X), T(X^2)}) = Span({3x, 2+ \frac{3}{2}x^2, 4x + x^3})$ 이 된다. 이 때, 세 원소는 서로 Linearly-independent하므로 rank(T) = dim(R(T)) = 3이다. 이 때, 공역의 Dimension은 $dim(P_3(R)) = 4$이므로, 공역과 치역은 달라진다. 따라서 T는 전사함수가 아니다.
- $nullity(T) + 치역 demension = 정의역 demension -> 0 + 3 = 3 = rank(T)$
-
Nullity는 0. Zero-vector 하나만을 원소로 가진다. 따라서 T는 one-to-one이다.
- 또한 one-to-one 함수는 image당 하나의 pre-image만 대응해야 하므로, nullity가 0라는 말은(Only Zero-vector) one-to-one이 되고 one-to-one이면 nullity가 0라고 할 수 있다.
S가 linearly independnt할 때, one-to-one이면 T(S)도 linearly independent하다.
-
T가 일반적으로 linear 하기만 하면, 이건 성립하지 않는다.
-
one-to-one(단사함수) 일 때는 가능하다.
-
$\sum_{i=1}^{n} a_i*T(v_i) = 0$ 일 때, T는 linear하니까 밖으로 빼줄 때, 이게 성립하려면 one-to-one이므로 nullspace일 때 밖에 없다. 따라서 $a_i = 0$여야 하므로, T(S)는 Linearly independent하다. 다시 말하자면, 이 식이 linearly dependent하다면, 좌측변에 $a_n$이 0이 아닌 애가 있어야 할텐데 그런애가 없으므로, Linearly independent하다고 할 수 있다.
Ex 13.
-
$T: P_2(R) \to R^3$ , $a_0 + a_1x + a_2x^2 \to (a_0, a_1, a_2)$ 일 때, 예시 넣어보면, S가 Linearly independent하다는 것을 증명 가능하다.
-
Basis를 LT했을 때 같은 곳으로 mapping 된다면, 그 공간에 속하는 나머지 원소들도 같은 곳으로 mapping된다. 너무 자명해서 설명은 생략.
정리
- LT의 성질
Properties of Lienar map
- $T(0) = 0$ (Zero vector 의 output은 Zero-vector이다) (즉 해당되는 공간의 벡터는 항등원 및 역원이 존재해야하고, 그렇게 되면 반드시 원점을 지나게 되므로, 당연히 Zero-vector의 Output은 Zero-vector가 된다.)
즉, 아래 그림은 Linear하지 않다.
-
$T(cx + y) = cT(x) + T(y)$
-
$T(x - y) = T(x) - T(y)$
-
$T(\sum_{i=1}^{n} a_i*x_i)$ = $(\sum_{i=1}^{n} a_i * T(x_i)$) -> 즉 스칼라곱을 미리하고 Linear transformation을 하나, 나중에 하나 같다는 것이다.
-
Reflection (-x1, y1) -> (x1, y1) 및 정사영도 LT이다.
-
Nullity는 Nullspace (치역이 zero가 되는 정의역의 집합)의 차원이고, Rank는 Range(치역)의 차원이 된다.
-
단사함수는 정의역이 서로 다를 때, 치역이 서로 다른 것. 즉 One-to-One. 일 대 일 매핑이라고 생각하면 된다.
-
전사함수는 치역과 공역이 같은 것을 의미한다.
Matrix representation
-
LT는 항상 행렬로 나타낼 수 있다.
-
$A = [T]^\gamma_\beta$는 ordered basis인 $\beta$를 LT인 T를 통해서 다른 ordered basis인 $\gamma$로 LT하겠다는 걸 나타낸다.
Ex.1
-
In $F^3, \beta = e_1, e_2, e_3$
-
$e_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ $e_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ $e_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$
-
$r = {e_2, e_1, e_3}$ 일 때 $\beta != \gamma$ 일 때
-
집합으로 보면 $\beta = \gamma$ 인데, oredered bases로 보면 서로 다르다.
Def.
-
V, W : Finite-dimensional vector space에서 $T:V \to W$ 일 때 V의 ordered basis $\beta = {v_1, v_2, …, v_n}, W의 ordered basis $\gamma = {w_1, w_2, …, w_m} 일 때
-
$T(v_j) = \sum_{i=1}^{m} a_ij w_i$로 표현이 가능하고, 이 때 $a_ij$를 통해서 이 LT를 행렬로 표현할 수 있다.
Ex.3
-
$T:R^2 \to R^3$일 때 $(a_1, a_2) \to (a_1 + 3a_2, 0, 2a_1 - 4a_2)$이면 $\beta$를 $R^2$의 Basis로 $\begin{pmatrix}1 & 0 \end{pmatrix}$, $\begin{pmatrix}0 & 1 \end{pmatrix}$이 되겠지) $\gamma$를 $R^3$의 Basis로 ($([1 0 0] [0 1 0] [0 0 1])$이 되겠지) 삼을 때, $([T]_\beta)^\gamma$를 어떻게 나타낼까?
-
$T(1, 0) = (1, 0, 2) = 1e_! + 0e+2 + 2e_3, T(0, 1) = (3, 0, -4) = 3e_1 + 0e_2 - 4e_3$으로 나타낼 수 있다. $e_n$은 물론, R^3의 Basis들이다.
-
이걸 나타내면 $\begin{pmatrix} 1 & 3 \\ 0 & 0 \\ 2 & -4 \end{pmatrix}$로 나타낼 수 있다.
-
만약, $r^prime$를 $e_3, e_2, e_1$으로 바꾼다면 단순히 행의 순서만 저것에 맞게 배치해주면 된다.
-
결론적으로는, 그냥 LT인데, 순서를 신경써라~ 이거다.
-
LT를 규정하고, 순서를 신경써서 하면 된다.
Def. LT의 모음은 그 자체가 Vector space가 된다.
Ex.5
- $T: R^2 \to R^3$이고, $U: R^2 \to R^3$ 일 때, 서로 LT식이 다르다고 해도, (T+U)의 LT 결과도 같다. 이게 당연한게, 예전에 이미 T(x+y) = T(x) + T(y)를 증명하지 않았던가
따라서 ordered basis가 적용된다고 해도, 이는 같다. 이와 유사하게 역시 Ordered basis라고 해도 cT(x) = T(cx) 역시 성립한다.
U * T * X 가 있을 때는, T와 X를 먼저 계산하고, 그 다음에 U와의 계산을 진행한다.
앞서 설명했지만, Ordered basis를 가지는 LT도 교환법칙 및 결합법칙이 모두 성립한다. 또한 Additivity 및 Homogeneouty 역시 성립한다.
Matrix multiplication
-
일반적으로 알고있는 행렬의 곱이다.
-
그렇다면 왜 이렇게 곱하는가?
-
$C = AB$이고, $C_ij = \sigma{k=0}^{m} A_ik B_kj$일 때, 이는 A원소와 B원소의 내적이(Dot product니까) C의 원소가 됨을 나타낸다.
-
이건 또 왜이럴까? 알아보기로 한다.
-
그 전에, 행렬의 곱이란 단순히 숫자를 그리드형태로 나타내어서 곱해주는게 아니라, 차원(Dimension)을 바꿔주는 것이란 걸 기억하자.
이해를 돕기 위한 예시 1
- 공간 $V, W, Z$가 있고, $V \to W$를 $T$, $W \to Z$를 $U$라고 할 때, $\alpha, \beta, \gamma$는 각각 $V, W, Z$의 Basis Vector를 의미한다고 하자.
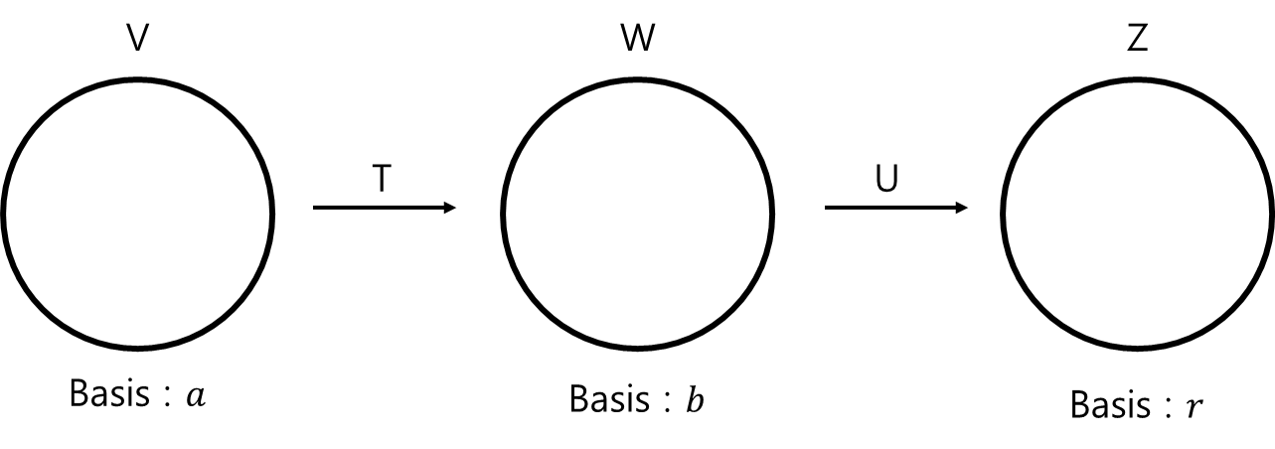
-
여기서 V에서 Z로가는 함수를 나타내려면, 두개의 LT를 거쳐야한다. 이 두 LT를 한 식으로 표현하려면?
-
행렬 곱으로 나타낼 수 있다 $\to$ $UT(\alpha) = U(T(\alpha))$
-
또한, $[T]^\beta_\gamma$를 B로 $[U]^\gamma_\beta$를 A로 나타낼 수 있다.
-
T를 먼저 처리해야하므로, T가 더 뒤에 있는걸 주의 (교환법칙이 성립하지 않는다.)
-
즉, 합성함수는 행렬 곱으로 나타낼 수 있다는 걸 알면된다.
-
또한 $(AB)^t = B^t A^t$를 기억하기.
Ex. 2
-
$U$는 미분(3차원 $\to$ 2차원), $T$는 정적분(2차원 $\to$ 3차원)이고, $\alpha, \beta$는 각각 3차원 및 2차원의 기저벡터가 된다.
-
따라서 $\alpha = 1, x, x^2, x^3$이 되고, $\beta = 1, x, x^2$이 된다.
-
$U$, 즉 미분을 어떻게 행렬식으로 나타낼까? 여기서는 3차원을 2차원으로 Projection 시키는 역할을 한다.
-
$U(\alpha)$는 $U(1) = 0, U(x) = 1, U(x^2) = 2x, U(x^3) = 3x^2$으로 나타낼 수 있으므로
-
U*변환 시킬 차원 이라고 생각하면 U는 $U = \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \end{pmatrix}$
-
로 나타낼 수 있다.
-
이유는 행렬 곱을 진행했을 때의 결과물은 3x4행렬 곱하기 4x1행렬은 3x1행렬이 되어서 한 차원 내려가므로 미분을 행렬로 나타냈다고 할 수 있겠다.
-
반대로 T는 $T(1) = x, T(x) = (x^2)/2, T(x^2) = (x^3)/3$으로 나타낼 수 있으므로 마찬가지로 T뒤에 변환시킬 차원이 곱해진다고 생각할 때
-
$T = \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1/2 & 0 \\ 0 & 0 & 1/3 \end{pmatrix}$라고 생각하면 된다.
-
즉, 쉽게 생각하면, LT는 행렬로 나타낼 수 있고, 차원 변환 행렬의 뒤에 원래 차원이 곱해지니까 차원 변환 행렬의 행은 바뀐 후의 차원을, 열은 바뀌기 전의 차원을 나타낸다고 생각하면 편할듯 하다.
Kronecker delta function
-
$\sigma_ij = 1 (i = j) / 2 (i != j)$
-
즉, Identity matrix는 이 Kronecker delta function으로 그대로 나타낼 수 있다. $\sigma_ij = I_ij$
Zero-divisor
-
조금 갑자기 나왔지만, 대수학에서는 중요한 개념.
-
$AB = 0$일 때, A도 B도 0가 아닐 수 있다.
-
다시 말하자면, 이건 약분이 안된다고 생각하면 된다.
-
항상 4로 나눈 나머지만 가지는 세상이 있다고 할 때, 2*2는 0이 된다. 2는 0이 아닌데도 말이다. 극단적인 예시이기는 하지만 저런식으로 디자인되는 케이스를 Zero-divisor라고 생각하면 된다.
Thm
- 위에 설명한 대로, 왼쪽에 LT를 곱해주는걸 Left multiplication transformation이라고 하고 A에 LT를 곱해주는 것을 $L_A$ 와 같이 나타낸다.
Invertibility
-
역함수를 구할 수 있느냐 없느냐를 의미.
-
$UT = TU = I$일 때, $U = T^-1$로 나타내고, T는 U의 Inverse라고 표현할 수 있다.
-
또한, 단사함수가 아니면 함수 정의가 안된다. 왜냐하면 Inverse했을 때 어떤 preimage로 가야하는지 모르기 때문이다.
-
또한, 전사함수가 아니어도 함수 정의가 안된다. 전사함수가 아니라는 것은 치역에 속하지 않는 공역이 있다는건데, 그건 역함수를 곱했을 때 preimage로 바뀔만한게 없기 때문이다.
-
따라서 T의 역함수를 구할 수 있다는 이야기는, T는 전단사함수라는 것과 같은 이야기가 된다.
정리
-
Ordered basis는 Polynomial으로 표현되어 있는 식을 좌표로 나타내기 위해서 필요한 basis이다.
-
Ordered basis는 좌표를 표현하는 것이므로, 집합처럼 나타나더라도 순서가 정해져 있다.
-
LT는 행렬곱으로 표현될 수 있다. Left multiplication transform의 경우 A를 LT한다고 할 때 $L_A$와 같이 표현한다.
-
Left multiplication transform의 경우 Transform matrix의 행이 바뀔 행렬의 차원-1이 된다. 열은 바뀌기 전 행렬의 차원-1이 된다.
-
LT를 먼저하고 Ordered basis를 통해 좌표로 표현하든, 좌표로 먼저 표현하고 LT를 하든, 결과는 같다.
-
행렬은 약분이 안된다. 정방행렬일 경우 역행렬을 통해서 구할 수는 있다. 아니면 Gauss 소거법을 통해 parameter를 얻어야 한다.
-
합성함수역시 행렬곱으로 표현할 수 있다. 다만, 주의해야 할 것은 먼저 곱해지는게 곱해지는 수와 가깝게 써야한다는 의미이다.
-
예를 들자면, L은 1->2차원, T는 2->3차원이고 A가 1차원 Vector일 때 Result = TL(A)가 되어야 하는 것이다.
-
역함수는 함수가 단사함수이자 전사함수이어야한다.
Invertibility
-
역함수가 존재하는지.
-
역함수가 존재하려면 저번 시간에 증명한대로, 전사함수이자, 단사함수가 되어야한다. 두 조건을 만족시키지 못하면, 어떻게든 Pre-image가 없는 Image들이 생기기 때문이다.
-
$(TU)^-1 = U^-1 T^-1$이어야 한다.
-
$(T^-1)^-1 = T$ 이어야 한다.
-
T라는 LT가 있고, $dim(V) = dim(W)$일 때 전사함수이자 단사함수여야한다.
Def.
-
V,W : Vector space일 때, T가 LT이고, $T: V -> W$를 취할 때, 이 LT의 역행렬이 존재하면 V와 W는 구조적으로 똑같은 Vector space이다.
-
위의 증명과 같이, 차원이 다르거나 하면 역행렬이 존재할 수가 없다.
-
이것을 V와 W가 Isomorphic하다고 표현한다.
Change of coordinate matrix (좌표 변환 행렬)
-
위 그림에서 나타나 있는 $x,y$ 좌표계를 $x’, y’$ 좌표계, 즉 타원을 표현하는 좌표계로 변환시키려고 한다.
-
이를 $x, y$를 사용해서 나타내려면, 제일 위에 있는 식처럼 4xy라는 합성함수가 붙지만, 제일 아래에 있는 식과 같이 좌표계를 변환함으로써 합성함수 없이 간단히 나타낼 수 있다.
-
이런 역할을 하는 행렬을 보통은 $Q$로 나타낸다.
-
Q는 항상 Invertable하다. 그 이유는 Q가 Identity Transformation의 행렬 Representation이기 때문이다. 즉, LT를 통해, 동일한 값이지만 차원을 변경한다고 생각하면 Q가 Identity transformation의 행렬 표현이라는 것에 대해서 감이 올 듯 하다.
Ex. 1
-
$\beta = (1, 1), (1, -1)$이고 ,$\beta’ = (2, 4), (3, 1)$이라 할 때
-
$[(2, 4)]_(\beta’) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$로 나타낼 수 있다.
-
이건 (2, 4)라는 벡터를 $\beta’$으로 나타내라는 문제인데, (2, 4)에다가 뭘 곱하면 $\beta’$이 될지를 생각해보면 [1, 0]이 되는 이유를 알 수 있다.
Def.
- $B = Q^-1 A Q$ 일 때, B와 A는 Similar하다고 표현한다. 이것은 즉, B와 A가 서로 같은 LT를 나타내고 있다는 뜻이다.
nxn elementary matrix
-
Identity matrix에 특정 Operation을 취해서 변환한 행렬을 의미한다.
-
이렇게 만들어진 행렬을 다른 행렬과 곱하면, 곱해진 행렬에 위의 그 ‘특정 Operation’을 취하게 된다.
-
즉, (3 x 3) Identity matrix의 2행 3행을 서로 바꾼 elementary matrix를 만들었다고 가정하자. 이걸 다른 행렬에 곱하면, 곱해진 그 행렬의 2행 3행을 바꾸는 역할을 하게 된다.
-
Elementary matrix 간의 곱은 Identity matrix가 된다. 한번 해보면 직관적으로 이해된다.
-
Elementary matrix는 항상 Invertable하다. (Inverse matrix는 물론 해당 Elementary matrix이다. 곱해서 Identity matrix가 되야할테니까)
Rank of Matrix
-
Matrix의 Rank는 Matrix의 Range의 Demension을 뜻한다. 따라서 이건 Matrix에 LT를 취했을 때의 Rank라고 볼 수 있으니, $rank(A) = rank(L_A)$ 가 된다.
-
이것에 대한 증명은 하지 않지만, LT를 행렬로 나타냈을 때 Range는 그 행렬의 Row space의 dimension이라고 할 수 있는데 이는 결과 행렬에도 선형적으로 적용될 것이므로 위 성질은 이해할 수 있을 것이다.
-
LT를 행렬로 나타냈을 때, 이 행렬이 Invertable matrix이면 원 행렬의 Rank가 그대로 유지된다.
-
이는 LT 행렬이 정방행렬이라는 것을 뜻하고, LT 행렬의 Rank가 Row의 개수와 같다는 것을 의미하기 때문에 원 행렬의 Rank가 그대로 유지되는 것이다.
-
만약 LT 행렬이 Invertable하다는 보장이 없으면, 행렬 곱이 거듭될 수록 행렬의 Rank는 계속 작아지게 되겠지.
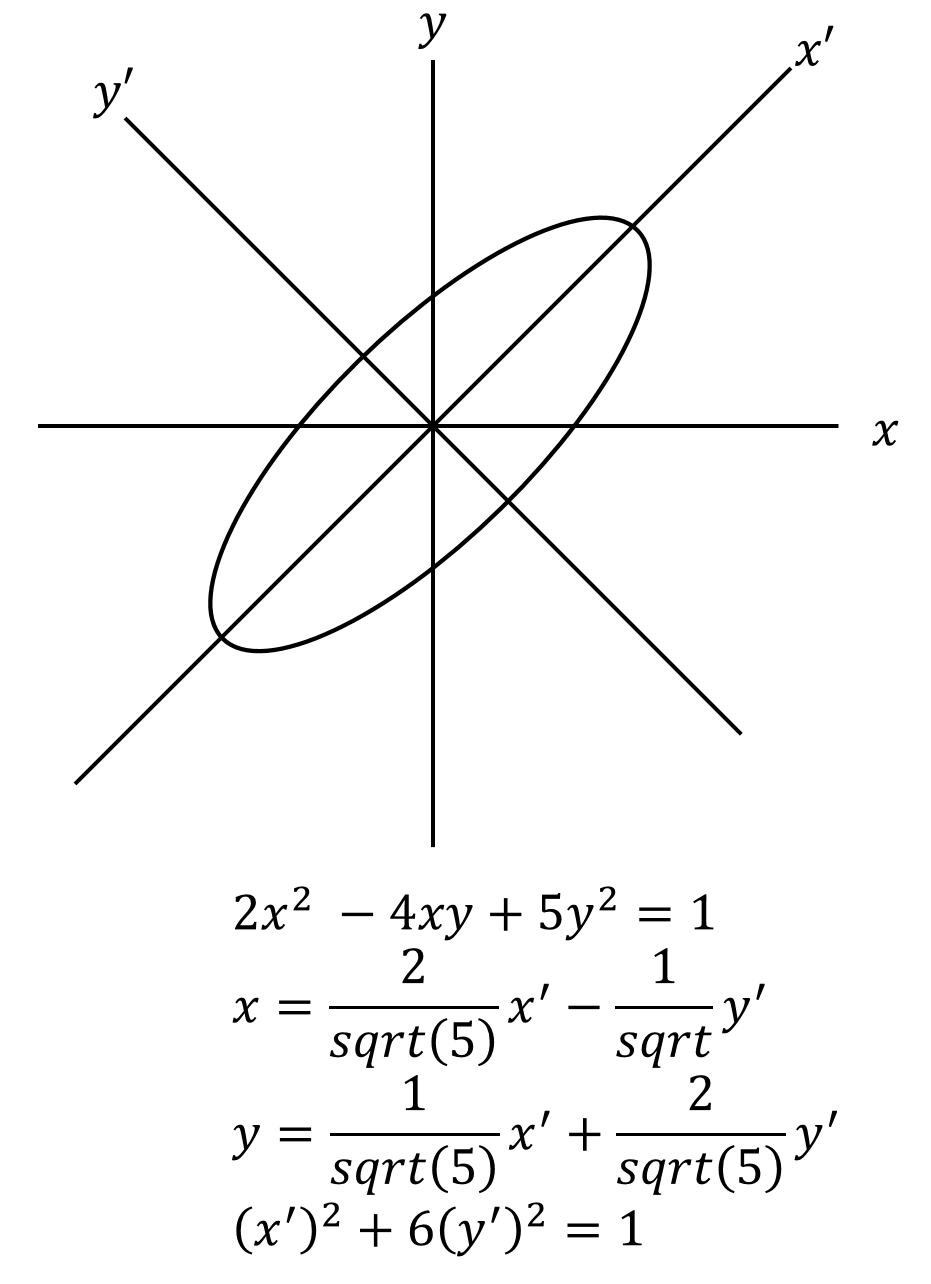

댓글남기기