[Linear algebra] Determinant
Linear algebra 4강
본 포스팅은 김영길 교수님의 유튜브 강의를 보고 개인적인 공부 목적으로 적은 것 임을 밝힙니다. 문제가 될 시 삭제하겠습니다.
목차
- Vector space
- Linear transformation and matrix
- System of linear equations
- Determinant
- Diagonalization
- Inner product space
Deterninant of order 2
-
Def. $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ 일 때, a, b, c, d는 Field의 원소일 때
-
determinant A를 det(A)로 표기하고, A의 절대값을 의미하며(= A ), 이는 위 행렬에서 $ad - bc$ 로 나타나게 된다. -
또한 determinant는 A를 이루는 두 벡터가 이루는 평행사변형의 넓이를 의미한다.
-
Determinant는 Additivity를 성립하지 않는다. 따라서 이는 Non-linear transformation이다.
- A의 determinant가 0이 아니면 A는 Invertable하다.
Ex 1.
-
$R^2$ 에서 기저벡터가 $u, v$ 일 때
-
det[u, v] / det[u, v] = +- 1이 된다. -
이는 두 벡터(차원 공간의 기저벡터)가 이루는 각이 시계 방향이냐(-1), 반시계 방향이냐(1)에 따라서 나뉜다.
- 두 벡터가 Independent할 때, 두 벡터의 determinent는 두 벡터가 이루는 평행사변형의 넓이가 되고, dependent하면 한 직선 내에 있는 것이므로 넓이가 0이 된다.
Area function
- 위에도 기술했듯이, 두 벡터의 determinant의 절대값은 두 벡터가 이루는 평행사변형의 넓이를 의미한다. (넓이는 항상 양수니까 절대값을 취하는 것이다.)
Determinant of order n
-
$A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$ 일 때
-
Submatrix는 $A^~_11$과 같이 표기하며, 이는 A의 1행 1열을 지우고 남은 행렬을 의미한다.
- 위 슬라이드는 n order matrix의 determinant를 구하는 방법을 설명하고 있다.
- 위 슬라이드와 같은 식으로 Determinant를 구하면 된다.
Corollary
-
어떤 행렬의 row나 column이 완전히 0이면 det(determinant)가 0이 된다.
-
이건, Cofactor를 0인 행 및 열로 구한다고 하면, 전부 0이 곱해지니까 0이 될 것 이니까 자명하다.
-
이것 또 당연한게, 하나의 행이나 열이 0이면, 이 식은 다른 식이랑 서로 mutually depenent할테니까 Invertable하지 못할 거고, 그러면 det가 0이 될 것이다.
-
또한, 두 개의 행이나 열이 서로 같으면 det가 0이 된다.
-
이것도 당연하지 Gaussian Elimination하면 한 행이나 열이 0이 되니까 위의 정리와 같이 적용되겠지.
Thm 4.6
-
어떤 행이나 열에 다른 행이나 열을 더하거나 빼더라도 det는 같다.
-
이 말은 어떤 의미를 띄냐면, 결국 det는 Pivot variable들의 곱으로 나타낼 수 있다는 것이다. 왜냐하면 다른 Free variable이 det에 영향을 주지 못하니까.
-
이것은 determinant를 구하는 데에는, cofactor를 구하는 것 보다 Gaussian Elimination을 하는게 더 좋다는 걸 뜻한다.
Type 2
-
어떤 하나의 Row나 Column에다가 Nonzero값 k를 곱하는 것을 Type 2 operation이라고 한다.
-
$Bk = A$일 때, $det(B) = kdet(A)$ 가 Type 2의 식.
-
만약에 하나의 Row나 Column이 아니라, B전체에 k를 곱하면 $det(kb) = k^ndet(a)$가 되겠지?
-
det할 때, 각 열에 곱이 들어가게 되니깐 그렇지.
Determinant of upper triangular matrix
-
대각선 밑의 성분은 전부 0일 때
-
$A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{pmatrix}$
-
Upper triangular matrix의 determinant는 Pivot variable의 곱이라고 할 수 있다.
-
왜냐하면 이 식은 이미 Echelon form을 만들어졌다고 할 수 있으니깐.
-
즉, 이 성질은 그냥 determinant를 구할려면, Gaussian elimination을 해서 행렬을 Echelon form으로 만들어주고, Pivot끼리의 곱, 즉 대각선 성분의 곱으로 Determinant를 구하면 편하다는 것을 말해준다.
-
Gaussian elimination 할 때, Row나 Column의 순서를 바꿀 때에는 det에 -1을 계속해서 곱해줘야한다는 사실을 잊지말기.
Properties of determinant
-
방금 말했지만, Row나 Column을 Exchange할 경우에는 det에 -1을 곱해줘야한다.
-
$det(AB) = det(A)det(B)$ 이다.
-
Invertable = nonsingular
Cramer’s rule
-
해를 구하는 방법 중 하나.
-
A가 square matrix이고, A가 nonsingular일 때
-
$Ax = b$를 풀 때, A의 Determinant가 0이 아닌경우.
-
$x_k = \frac{det(M_k)}{det(A)}$
-
여기서 $M_k$ 란, A의 k번째 Column을 b로 치환한 matrix를 의미한다.
Cramer’s rule 예제
-
$\begin{pmatrix} 1 & 2 & 3 \\ 1 & 0 & 1 \\ 1 & 1 & -1 \end{pmatrix}$ $\begin{pmatrix} x1 \\ x2 \\ x3 \end{pmatrix}$ $= \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}$ 일 때
-
$x_1 = \frac{det(M_1)}{det(A)}$
-
= $\begin{pmatrix} 2 & 2 & 3 \\ 3 & 0 & 1 \\ 1 & 1 & -1 \end{pmatrix}$ div $det(A)$
-
$x_2 = \frac{det(M_2)}{det(A)}$
-
사실, 계산이 복잡해서 잘 안쓴다.
-
그냥 알아만 두자.
Determinant가 의미하는 것.
-
3x3 matrix일 때는, determinant가 무엇을 의미하는가?
-
2x2 matrix일 때의, determinant는 평행사변형이었지.
-
3x3의 determinant가 의미하는 바는 평행 6면체를 의미한다.

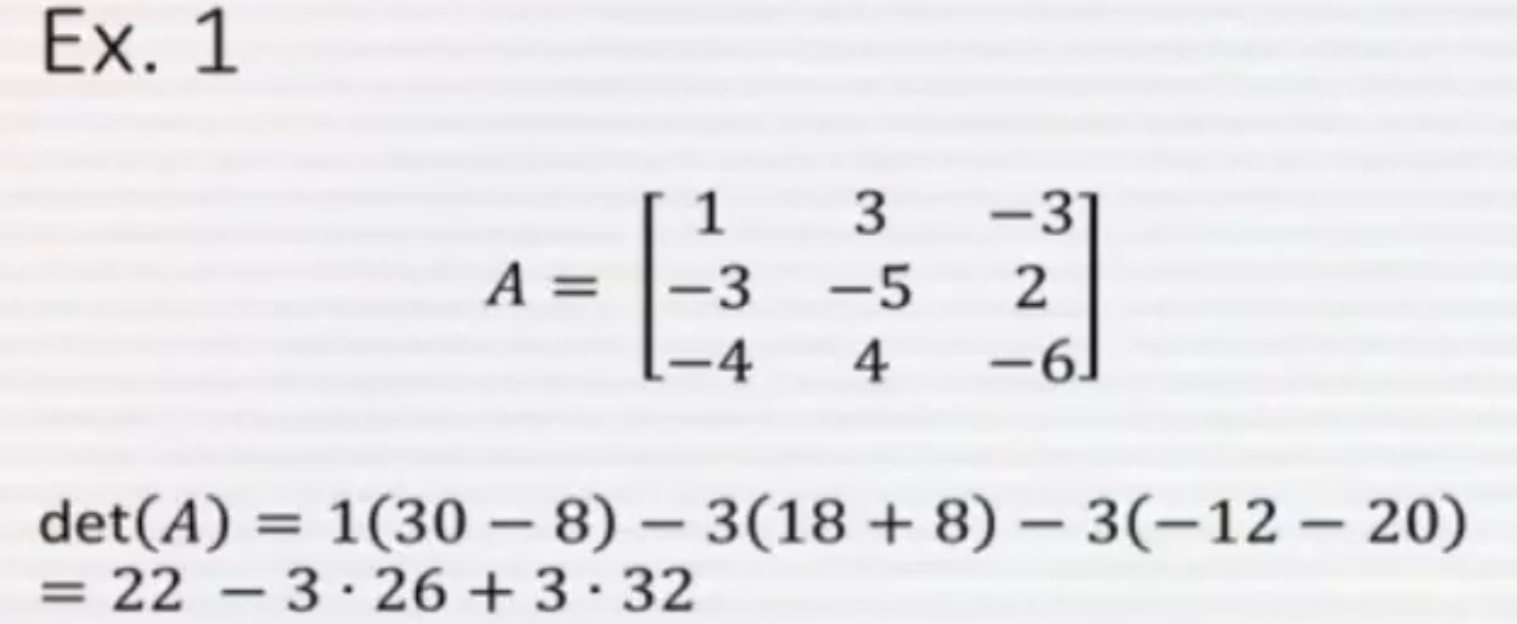

댓글남기기