[Pattern recognition] Linear regression & Classification

시작하기전에

본 포스팅은 패턴인식 수업 수강 후 Linear regression & Classification 에 대한 기본적인 지식들에 대해 복습할 기회 제공을 위해 개인적으로 만든 복습 문제 및 정답 포스팅입니다.

Questions

1. What is the formula for optimal goal of linear regression?

2. What is the formula for realistic goal of linear regression?

3. What is the differentiate of matrix?

4. What is the Normal-equation?

5. Can we optimize the Normal-equation?

6. What is the Hessian-matrix? (Machine learning perspective)

7. What is the parameter?

8. What is the hyper-parameter?

9. What is the formula of gradient descent?

Answer

1. $E_out (h)=E[(h(x)-y)^2]$

• Finding $h(x)$ for optimizing $E_out(h)$

1. $E_in (h)=1/N Ssigma_{n=0}^{N}$

• $(h(x_n )-y_n )^2 = 1/N \Sigma_(n=1)^N$

• $(w^T x_n-y_n )^2=1/N

  (

  Xw-y

  )

  ^2$

• $h(x)= \Sigma_(i=0)^d w_i x_i=w^T x$

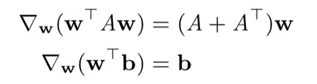
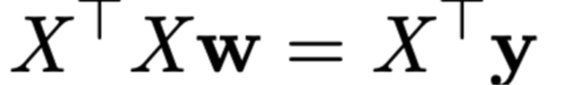
1. If $X^T X$ can be invertable, W can have unique solution. Or W can have non-unique solution.

2. The matrix able to proving that loss is convex.

3. The variables optimized by machine.

4. The variables determined by human.

5. $w(t+1) = w(t) - n\nabla(E_(train(w(t))))$.