[Concept summary] L1, L2 Norm/Loss/Regularization
Norm 이란?
- 선형대수학에서 벡터의 길이 혹은 크기를 나타낼 수 있는 방법
L1-Norm
-
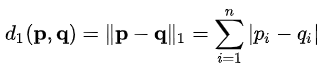
-
두 벡터의 각 원소들의 절대 차의 합
-
두 벡터를 $P_i, Q_i$로 나타낼 때,
-
$\P_i = (1, 2, -3), Q_i = (2, 3, 4)$ 이면 L1-Norm은 $|1-2 + 2-3 + -3-4 = 9$이다. -
Solution이 Non-trivial하다. 이는 경우에 따라서는 같은 효과를 낼 수 있는 방법이 여러가지가 될 수 있다는 것을 의미한다.
- 같은 효과를 낼 수 있는 방법이 딥러닝에서는 Weight의 Selection이 여러개 가능하다고 생각할 수 있고, 이런면에서 볼 때 L1-Norm은 Feature selection에 효과적이라고 할 수 있다.
L2-Norm (Euclidean norm)
-
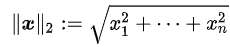
-
두 벡터의 직선 거리 (Euclidean distance)
-
두 벡터를 $P_i, Q_i$로 나타낼 때, $P_i = (1, 2, -3), Q_i = (2, 3, 4)$ 이면 L2-Norm은 $\sqrt{(1-2)^2 + (2-3)^2 + (-3-4)^2} = 3$이다.
-
Trivial solution을 가진다.
L1 & L2 Norm visualization
-
-
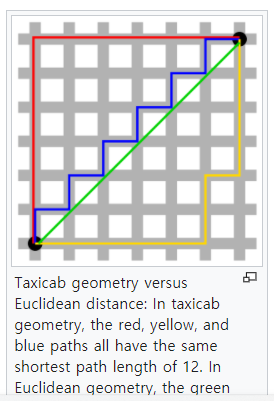
붉은색, 파란색, 노란색 라인은 L1-Norm으로, 모두 길이가 같다.
-
초록색 라인은 L2-Norm으로 L1-Norm에 비해 가장 Value가 작다.
L1-Loss (Mean Absolute Error - MAE)
-
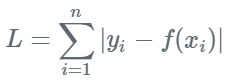
-
실제 Ground truth $y_i$, 예측 값(f(x_i)) 간의 절대 차의 합을 Loss로 사용
-
절대 차의 합을 Loss로 사용하는 만큼, 예측 값이 GT(Ground Truth)보다 높은지, 낮은지를 분간할 수 없음.
-
L2-Loss에 비해서 특이 값에 영향을 덜 받음.
-
절대값을 취하는 만큼 0인 지점에서 미분 불가능해서 Gradient-based method 사용시에는 주의 필요.
L2-Loss (Mean Squared Error - MSE)
-
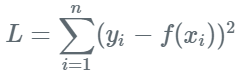
-
Regression에서 흔히 사용되는 L2-Loss(MSE)이다.
-
실제 Ground truth $y_i$, 예측 값(f(x_i)) 간의 차의 제곱의 합을 Loss로 사용
-
역시 제곱을 하므로 모델의 Prediction이 실제보다 낮게나오는지 높게나오는지를 판단 불가
-
제곱을 취하므로, MAE에 비해서 특이값이 취약함
-
우리가 알고있는 분산에 해당
L1-Regularization (Lasso)
-
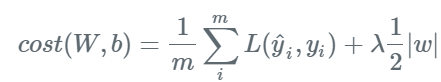
-
$\lambda$는 Coefficient. 클 수록 정규화 효과가 강해진다.
-
기존 Loss에 해당 가중치의 절대값을 더해준 형태
-
Loss에 가중치의 절대값을 더해준 만큼 학습 데이터에 너무 과대적합 되는 것을 방지해준다.
-
또한 계속해서 상수 값 (가중치의 절대값 * 상수)을 더해서 Loss를 만드는 만큼, 계속해서 가중치를 작게 만든다.
-
이는 작은 값의 가중치는 0으로 수렴하게 만들고, 결국 큰 가중치만 남기게 되어서 가중치들을 좀 더 Sparse하게 만든다.
-
따라서 L1-Regularization은 Sparse coding에 유용하게 사용된다.
L2-Regularization (Ridge)
-
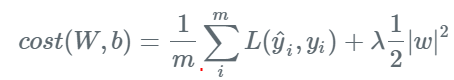
-
$\lambda$는 Coefficient. 클 수록 정규화 효과가 강해진다.
-
기존 Loss에 해당 가중치의 제곱을 더해준 형태.
-
역시 과대적합을 방지하는데 도움을 준다.
-
제곱을 하는만큼 L1 Regularization에 비해서 가중치의 영향이 더 크다.
-
Weight decay라고 부른다.
-
Trivial solution을 가진다.
-
범용으로 쓰기 좋아서 많이 사용된다.
Reference
-
https://en.wikipedia.org/wiki/Taxicab_geometry
-
https://en.wikipedia.org/wiki/Norm_(mathematics)
-
https://www.stand-firm-peter.me/2018/09/24/l1l2/

댓글남기기