[Pattern recognition] Feasibility of Learning

시작하기전에

본 포스팅은 패턴인식 수업 수강 후 Feasibility of Learning에 대한 기본적인 지식들에 대해 복습할 기회 제공을 위해 개인적으로 만든 복습 문제 및 정답 포스팅입니다.

Questions

1. What is the hoeffding-Enequality?

2. What is the learning?

3. What is the in-sample error?

4. What is the out-of-sample error?

5. What is the Union-Bound?

6. Describe the uniform version of hoessding-Eneqaulity.

7. What is the ultimate goal of the machine learning?

8. How we can do Feasibility of Learning well?

9. What is the sample complexity?

10. What is the hypothesis complexity?

11. What is the condition of hypothesis when $E_{in} ~= E_{out} $ ?

12. What is the condition of hypothesis when $E_{in} ~= 0$ ?

13. What is the compact between 11, 12 ?

14. What is the point-wise error?

15. What is the overall error?

16. How we measure the error?

17. What is the difference between the interpolation and regression?

18. What is the P(y

    x) ?

19. What is the $P(x)$ ?

20. What is the PAC ?

Answer

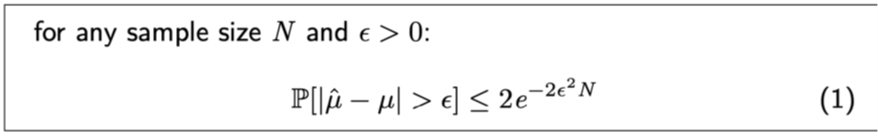
1. The estimation of Target value for using prediction.

   • $u, u^^$ is the prediction value and target value.

   • The $P$ is probility of bad event.

   • N is the size of dataset.

   • If N is high enough, $u, u^^$ will be similar than that N was small.

   • And if $\epsilon$ is high, the approximation of $u$ is better. But we need more sample.

2. The process finding optimal hypothesis in the hypothesis set.

3. The probability that the result deduced from the hypothesis is wrong in the data for which I know the correct answer.

   

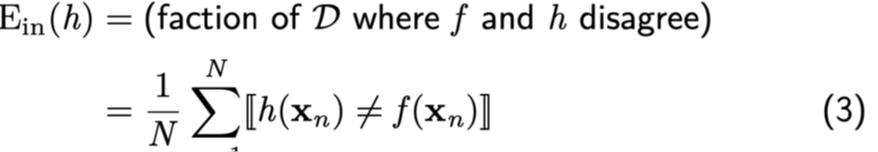
4. Probability that the inferred result from a population I do not know is not the same as the target function.

   

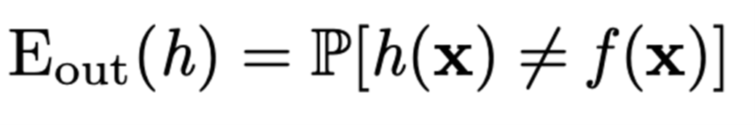
5. $P[A \cup B] <= P[A] + P[B]$

6. The version of multi hypothesises. Is has meaning when the hypothesis set is finite.

   • $P[E_{in}(g)-E_{out}(g)>\epsilon ]<= 2Me^(-2*\epsilon^2 N)$

7. Minimize the $E_{out}(g) ~= 0$

   • But it can not be real because our model has dependency in dataset.

8. Two condition.

   • $E_{out}(g) ~= E_{in}(g)$

   • $E_{in}$ must be small enough.

9. The number of training example.

10. The number of Hypothesises.

11. The hypothesis must be less complex. You can figure out with 6.

12. The hypothesis must be complex. Although there is a danger of overfitting, a complexity is required for reducing error.

13. Approximation-Generalization trade-off.

14. The error of each sample.

15. The average of point-wise error.

16. False accept, False reject.

17. Interpolation means a method that satisfies all samples. Machine learning x.

- Target function exactly satisfies y_n. That is, E_in=0.

- Regression does not satisfy all samples. Machine learning o

1. The target distribution cared for noise.

2. Input distribution.

3. Probably approximately correct.