[Concept summary] Cross-Entropy
Cross-Entropy (CE)
시작하기전에
- 개인 공부 목적으로 정리한 글입니다. 설명이 부족할 수 있습니다.
Cross-Entropy란?
-
Loss function중 하나. Input 값(=Model의 Output값)이 일반적으로는 확률로써 들어가기 때문에 Activation function이 주로 Sigmoid나 Softmax가 된다.
-
이 중 Entropy란, 불확실성을 나타내는 수치로써, output이 뭐가 나올지 얼마나 예측하기 힘든지를 나타내는 수치라고 생각하면 된다.
-
이 때, 우리는 Label의 entropy와 model의 output의 entropy의 곱을 통해서 현재 모델이 얼마나 정답을 예측하기 힘들어하는지를 Loss로 나타내고, 이를 통해서 학습을 진행하는 것이다.
-
공식은 아래와 같다.
-
$- \Sigma_{i=0}^{n}{L_i*log(O_i)}$ (이산형일 때, 연속형이라면 $\Sigma$ 대신에 $\integral$ 이 들어간다.)
-
$Term : L_i$ = i번 째 Label / $O_i$ = i번 째 model의 Output
-
위의 식은 i번째 label이 1일 때, 즉 정답에 속한 예측값일 때에만 loss가 0보다 커진다는 것을 알 수 있다.
-
즉, positive sample에 관해서만 학습을 하겠다 그 말이다.
-
-
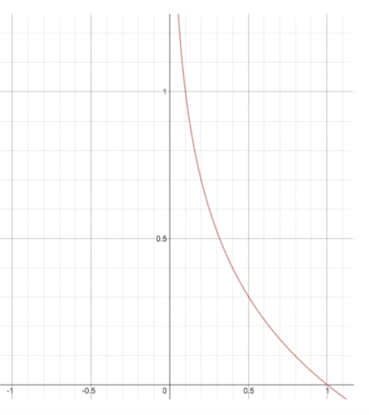
Cross entropy는 -Log(x)를 통해 어떤 input이 어떤 loss로 반환되는지를 쉽게 알 수 있다.
-
보면 x값, 즉 model의 output이 1에 가까우면 가까울 수록 반환값은 0에 가까워진다.
-
즉, label이 1일 때, output이 1에 가깝게 예측하면 낮은 loss를, output이 0에 가깝게 예측하면 무한대에 가까운 loss를 반환함으로써 학습을 하는 것이다.
-
실제로는 output이 sigmoid나 softmax에 의해서 도출된 확률 값이 들어가니까 One-hot encoding을 하지 않는 이상 loss가 무한대가 되진 않겠지만, 중요한 점은 잘 맞췄을 때는 loss가 0에 가까워지고, 못 맞췄을 때는 loss가 무한대에 가까워 진다는 점이다.
-
실제로 도출되는 loss는 $O_i$가 확률값인 만큼, (정말 작더라도) log(0.0000000001) ~ (가장 클 때에도) log(1)사이의 값을 가질 것이다. 즉, 0 ~ 10 사이의 값이 도출되는 것이 평균이 될 것이다.
-
이러한 과정을 통해서, Label 값이 정해진 것에 대해서만 학습을 진행한다. 이는 Binary classification이 아니라 Multi-Class classification (Label의 종류가 여러가지 인 것)이나 Multi-Label classification (한 image 내에 Label이 여러개인 것) 에도 동일하게 적용이 된다.
Cross-entropy 사용 시 Activation function 선택 방법
-
Cross-Entropy와 같이 자주사용되는 activation function은 ‘Sigmoid’와 ‘Softmax’ 두 개가 있다.
-
Sigmoid
-
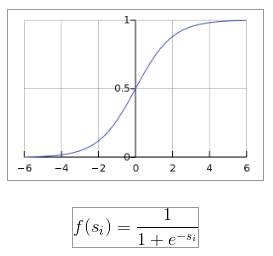
-
Softmax
-
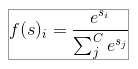
-
특징으로는 sigmoid는 값을 0~1 사이의 값으로 바꿔준다. Sigmoid는 모든 class에 대한 확률의 합이 1은 아니기 때문에, 주로 multi-class classification에서는 사용하지 않고, binary cross-entropy에서 자주 사용한다.
-
softmax역시 값을 0~1사이의 값으로 바꿔주지만, softmax는 모든 class에 대한 확률의 합이 1이기 때문에, 주로 multi-class classification에서 자주 활용한다.
Object detection network (Anchor-based)에서의 Cross-Entropy
-
여기서 의문점이 들 수가 있다. Label 값이 정해진 것에 대해서만 학습을 진행한다면, Anchor based detection network에서는 배경 부분은 아에 학습 안하는건가?
-
네트워크에 따라서 정하기 나름이지만, 어떤 사람은 배경 부분을 하나의 Class로 설정하고 학습하는 사람도 있고, 배경 부분을 고려한 Cross-entropy 식을 따로 규정한 사람도 있다.
-
따로 규정한 식은 아래와 같다. (출처 : Focal loss 논문)
-
-
여기서 $p_t$는 객체가 있을 확률을 의미하는 것으로, 만약 배경 부분을 예측할 경우 0에 가깝게 예측하면 loss가 낮아지도록 만들어 둔 loss function 이다.
-
다만, 이렇게 진행할 경우, anchor-based 방식에서는 배경 부분에 해당하는 sample이 압도적으로 많기 때문에, 배경 부분을 학습할 때에는 좀 더 penalty를 준다거나 하는 방식을 사용했다.
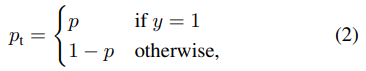

댓글남기기