[Concept summary] Cost(Loss) function의 종류 및 특징

2 분 소요

Cost(Loss) function

시작하기전에

이 글은 Cost function의 종류를 정리하고, 상황에 맞는 Cost function 사용을 위해서 적는 글이기 때문에

차근차근 가르쳐주는 글이 아니라는 것을 먼저 말씀드리고 싶습니다.

또한 아직까지 부족한 점이 많고, 컴퓨터 비전 관련 분야에 초점을 맞춰 딥러닝을 공부했기에

이 글에는 틀리거나 모호한 표현이 있을 수 있습니다.

혹시라도 눈에 띄게 되어 말씀해주신다면, 정말로 감사히 듣고 수정하도록 하겠습니다.

Cost function이란?

일반적으로 딥러닝에서는 정보의 속성에 대한 판별이나 정보를 기반으로 한 원하는 목적값을 추정하는 것이 목표가 됩니다.

여기에서 Cost function이 하는 일은,

현재 우리가 설계한 모델이 얼마나 이 데이터를 정확하게 표현하지 못하는 가를 수치적으로 나타내는 것 이라고 보시면 됩니다.

Cost function의 종류 - 1. for Regression

Cost function 그 목적에 따라서 여러가지로 분류되며

첫 번째 순서로는 Regression에 관한 cost function에 대해서 알아보겠습니다.

Regression에 관한 cost function들은 모두 비슷한 형태를 띄고 있습니다.

모두 label값과 prediction 값의 차이를 줄임으로써

Prediction을 label 값에 가깝게 만들어 모델을 완성하는 그런 cost function으로 이해하시면 될 듯 싶습니다.

  1. MAE (Mean Absolute Error)

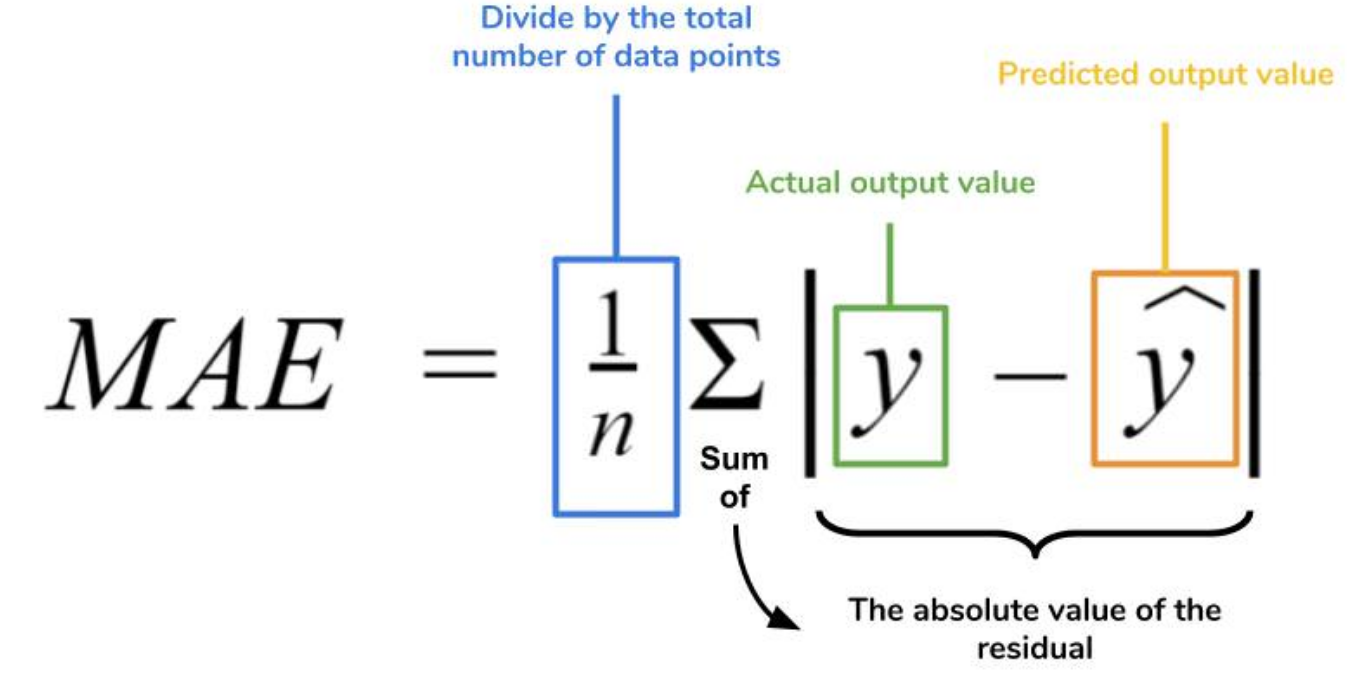
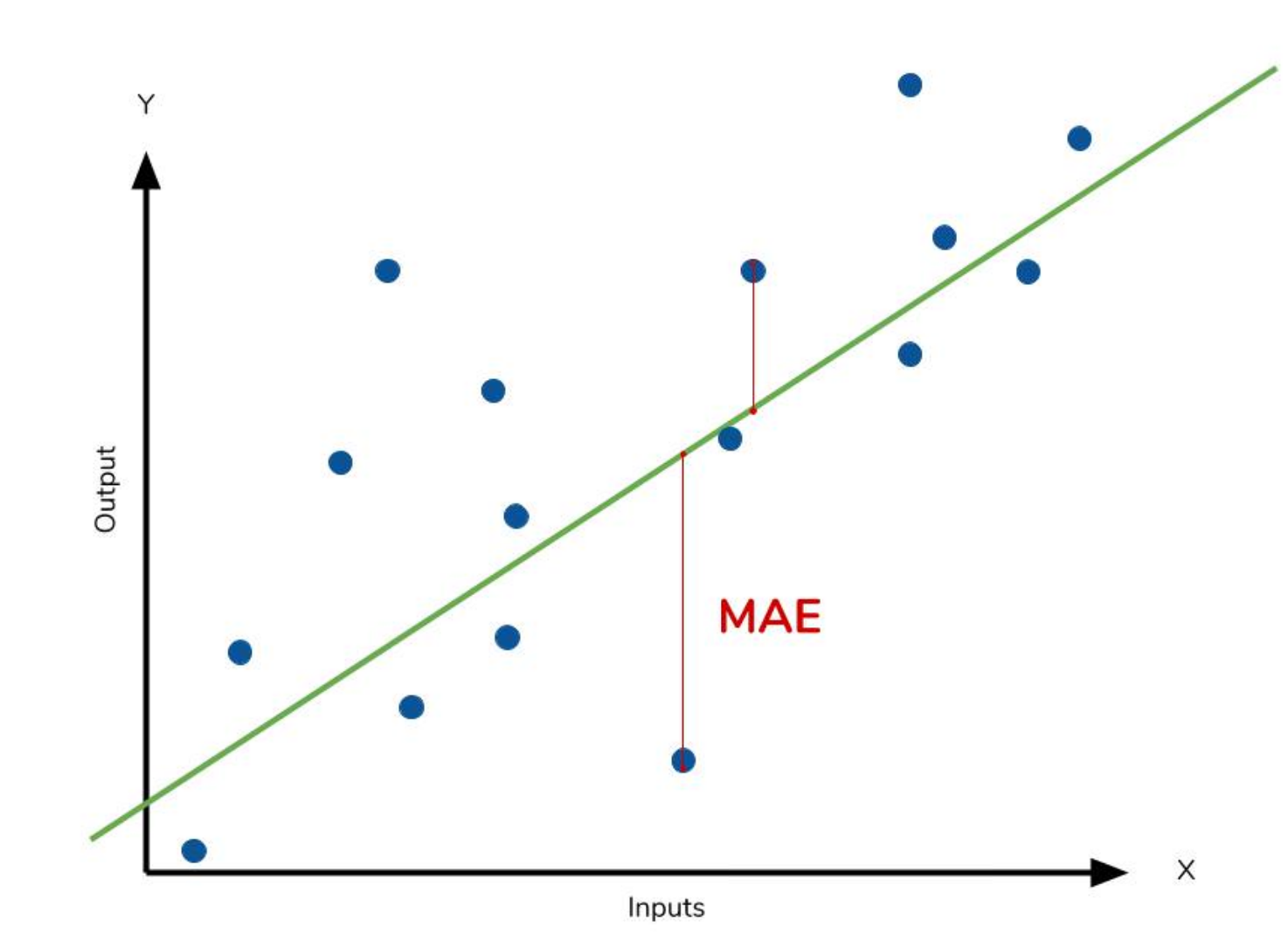
MAE MAE

  • 데이터와 모델 Prediction의 절대적인 차이 값의 평균

  • 절대값을 씌우므로 모델의 Output이 실제보다 낮게나오는지 높게나오는지를 판단 불가

  • 특이값이 많은 경우에 유용

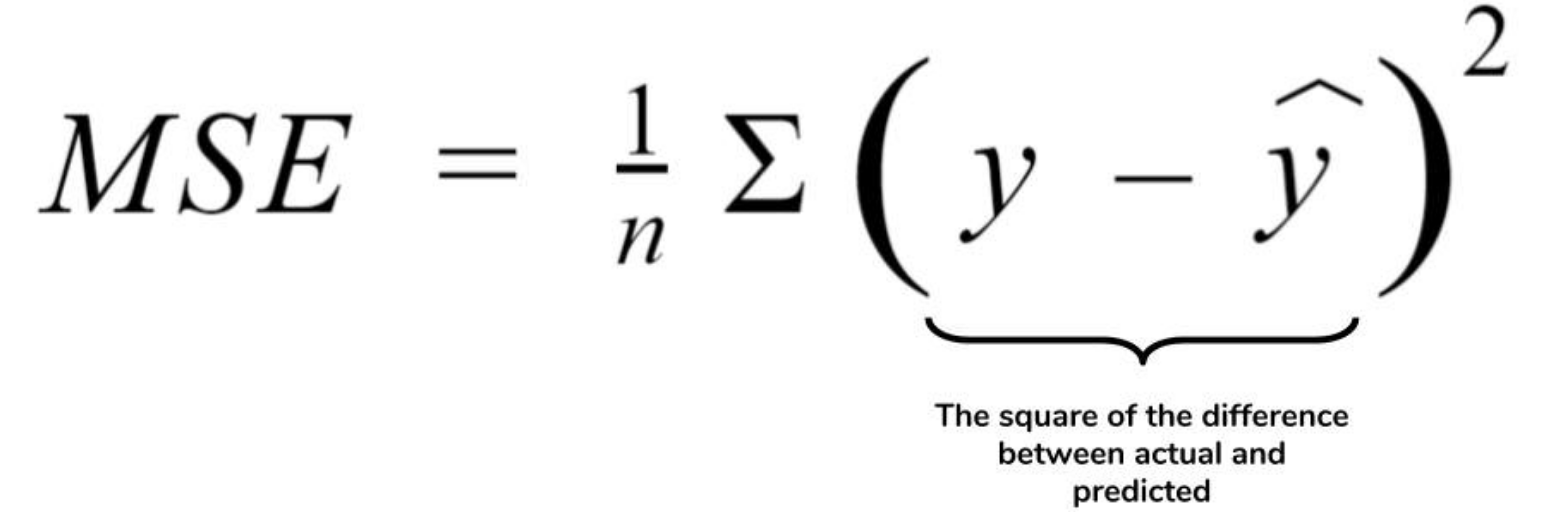
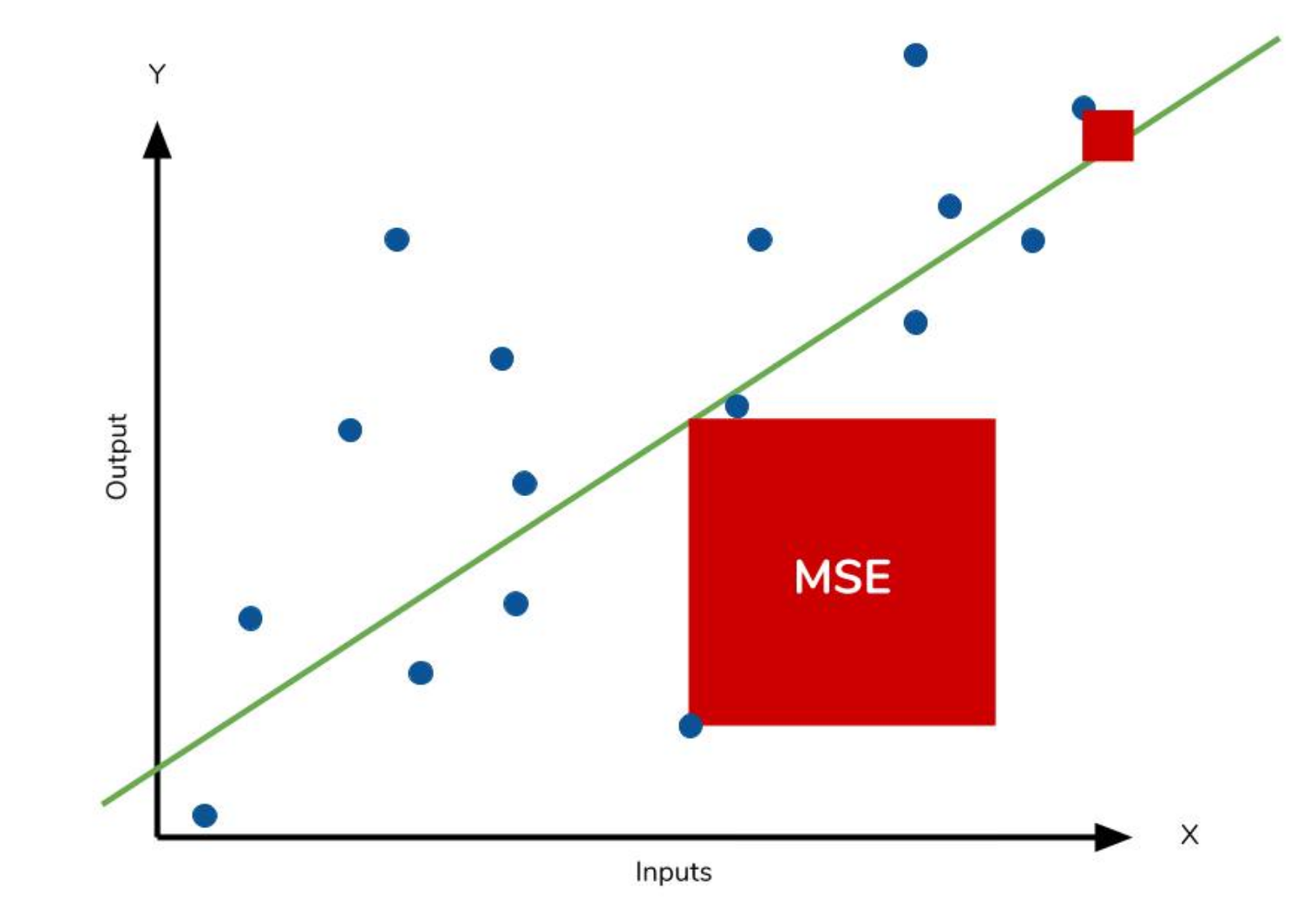
  1. MSE (Mean Squared Error) MAE MAE

  • (데이터와 모델 Prediction의 차이)의 제곱의 평균

  • 역시 제곱을 하므로 모델의 Prediction이 실제보다 낮게나오는지 높게나오는지를 판단 불가

  • 제곱을 취하므로, MAE에 비해서 특이값이 취약함

  • 우리가 알고있는 분산에 해당

  1. RMSE (Root Mean Squared Error) MAE

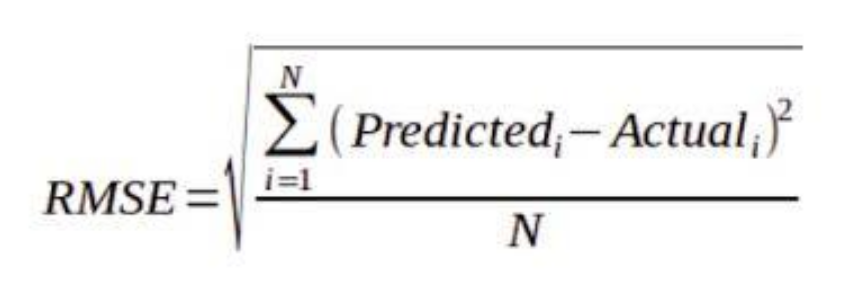
  • MSE와 매우 유사

  • 겉에 루트를 취함으로써 원래 입/출력과 유사한 값을 나오게 하여 직관성을 더해줌

  • 역시 특이치에 취약

  • 일반적으로 사용되는 Cost function

  1. MSLE (Mean Squared Log Error) MAE

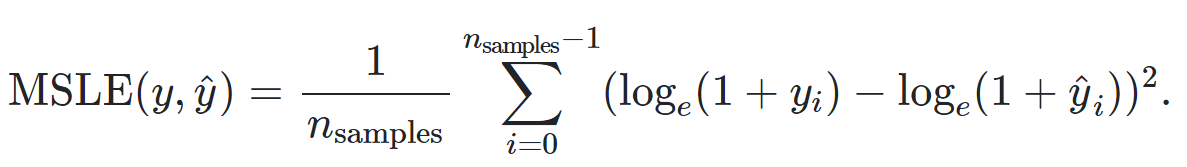
  • MAE에서 Prediction과 Label에 자연로그를 취한 형태

  • 기하급수적으로 커지는 데이터(인구수, 상품판매량)에 사용하기 좋음 (자연로그를 취하므로 과도하게 커진 특이값에 불이익을 주기 때문)

  1. MAD (Median Absolute Deviation) MAE

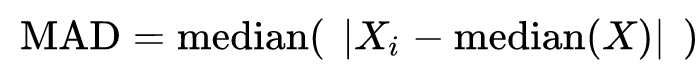
  • 각 값에서 중앙값을 빼고, 그 차이에 절대값을 취한 값들의 중앙값을 구합니다.

  • 특이치에 매우 강합니다.

Cost function의 종류 - 2. for Classification

  1. CE(Cross-Entropy) MAE

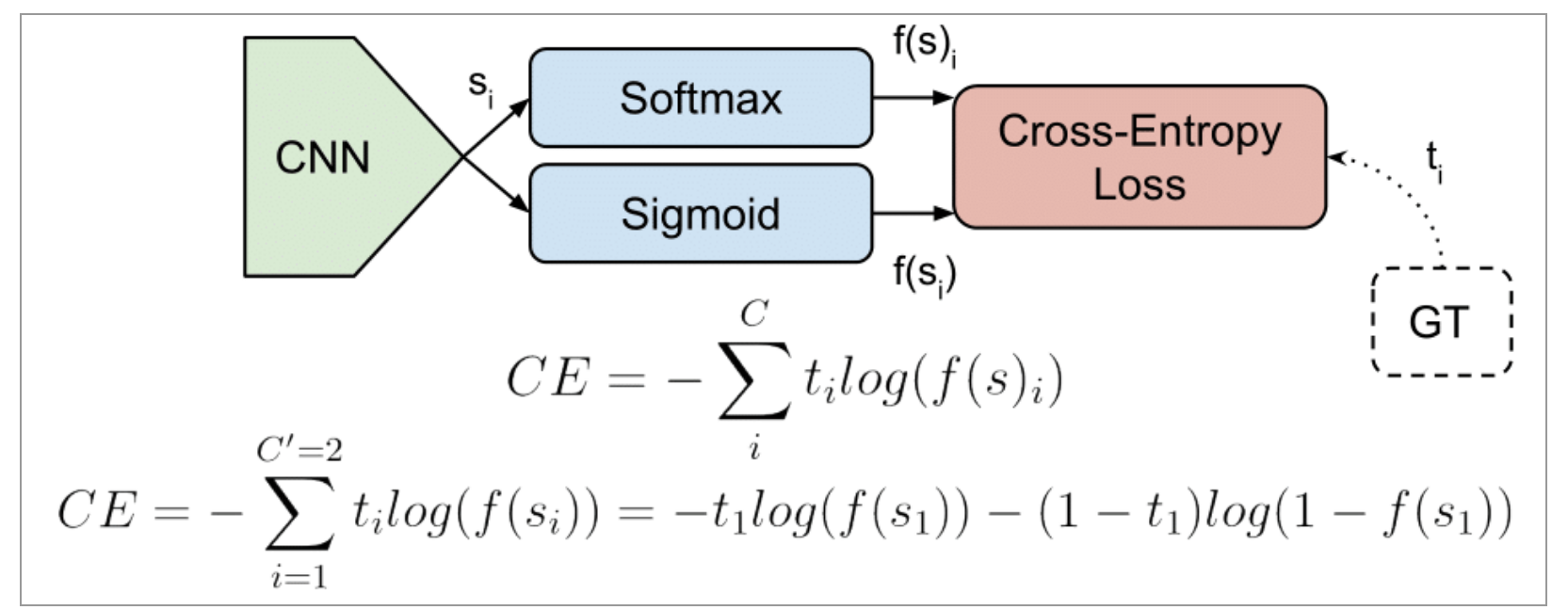
  • 두 식중 윗 식이 Cross-entropy의 식입니다.

  • ti가 label값, si가 prediction 값입니다.

  • 아랫 식은 윗식에서 C=2일 때, 즉 Binary-classification일 때를 의미합니다.

  • Softmax나 Sigmoid에 Onehot Encoding을 붙이고 그 후에 이 CE cost function을 자주 사용하곤 합니다.

(이 CE에 대해서는 그냥 넘어가셔도 좋지만 여기에서 자세한 설명을 보실 수 있습니다.)

간단한 설명만 덧붙여두자면, Entropy란 정보량의 불확실성을 의미합니다.

우리가 하고자 하는것은 정보량의 불확실성을 최소화하고, 쉽게 classification을 할 수 있는 환경을 만드는 것이 목적입니다.

여기서 불확실성을 최소화하기 위해서는 Input이 어떤 class인지를 나타내는 확률에(이미 fix)

그것에 최적화된 로직(changable)을 적용하는 것이 핵심입니다.

이 두개가 곱해져야 가장 적은 수가 나오고, 이것은 곧 가장 적은 cost로 이어지게 됩니다.

원래는 label에 맞는 최적의 로직이 따로 있지만, 현재의 우리는 si의 로직을 사용하고 있고

그 로직을 개선해야합니다.

여기에서의 Input이 어떤 class인지를 나타내는 확률이란 ti 즉 label값을 의미하고

거기에 곱해지는 로직이 바로 si입니다.

이 때 entropy가 최소화 되는 방향으로 si를 변화시킵니다.

즉, label 값에 맞는 로직을 찾는 것이 곧 정보량의 불확실성을 낮추는 것이 되고

그게 곧 올바른 classification을 위한 이상적인 방향이라서 Cross-entropy가 cost function으로서 작용하는 것 입니다.

이해가 잘 안되신다면 바로 위의 링크를 타고 가셔서 한번 읽으시면 이해가 되실 듯 싶습니다.

  1. KL-Divergence MAE

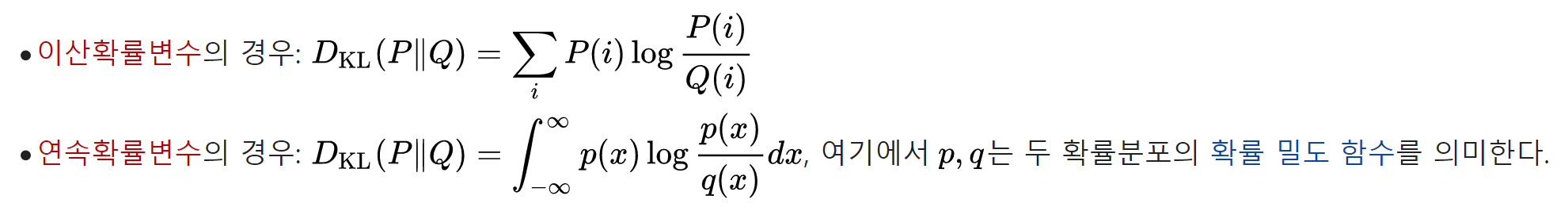
  • KL-Divergence는 Cross-entropy에서 원래 이상적인 로직 대신에 si의 로직을 사용했을 때의 차이를 의미합니다.

  • 즉 Cross-entropy의 cost를 의미합니다.

아직 미완성된 글입니다.

댓글남기기

참고