[Graphics] Projection Matrices: What You Need to Know First
시작하기전에
-
이 글은 Scratchapixel 2.0의 글을 개인 공부 목적으로 번역 및 요약한 글입니다.
-
https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matrices-what-you-need-to-know-first
Converting the Perspective Frustum to a Unit Cube
-
이전 강의에서는 상하좌우만 다루었지만 Z좌표에 대한 설명도 하겠다.
-
Z좌표가 Projection matrix를 거치면 API에 따라서 [0 1]이나 [-1 1] Range로 Mapping 된다.
-
Z좌표가 Near plane에 가까이 있으면 0 or -1로 Mapping되고, Far plane에 가까이 있으면 1로 Mapping 된다. (?)
-
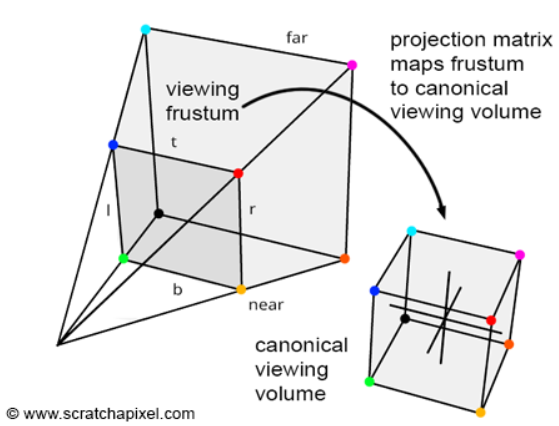
이렇게 3D Point를 모두 Projection 시키면 Frustum에 있던 좌표들은 2x2x1([0 1]) or 2x2x2([-1 1]) Cube로 Mapping 되게 된다.
-
이는 아래 그림과 같이 나타난다.
-
Point (x, y, z) = (2, 5, 10)를 Projection 하면, $x’ = \frac{2}{-10} = -0.2, y’ = \frac{5}{-10} = -0.5$가 된다.
-
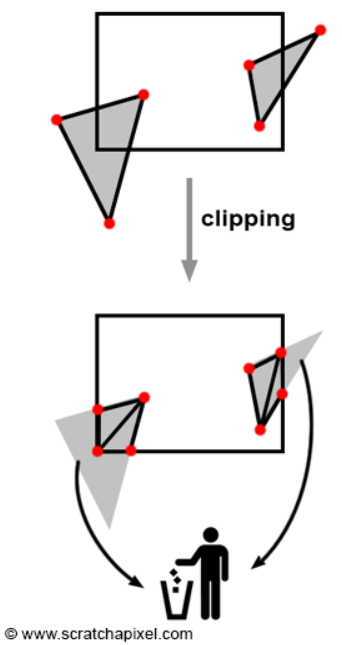
만약 Point가 Frustum 밖에 위치하고 있다면, 아래 그림과 같이 나타나게 된다.
- 이렇게 자르고 변환하고 하면, 위의 예시에서 이미 봤겠지만, 양수가 음수가 되고, 음수가 양수가 되곤 한다.
Procedure for projection
-
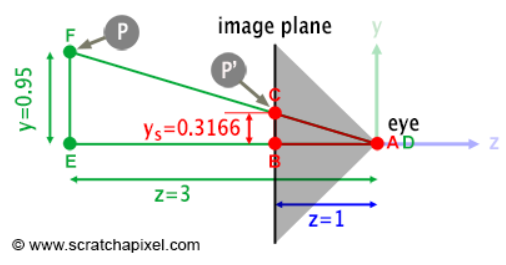
위 그림에서 P를 NDC로 투영하고 싶을 때, 투영된 점을 P’라고 할 때, 두 점을 포함하는 삼각형은 그림과 같이 닮음 관계에 있다.
-
따라서 $\frac{BC}{EF} = \frac{AB}{DE}$이다.
-
이는 $BC = \frac{AB*EF}{DE}$로 나타낼 수 있다.
-
또한 AB = 1이므로 $BC = \frac{EF}{DE}$이다.
-
이 식을 통해서, 우리는 X좌표든 Y좌표든 그냥 -Z값으로 나눠주기만 하면 NDC로 Mapping 된다는 것을 알 수 있따.
-
따라서 $(P_x)’ = \frac{P_x}{-P_z}$
-
$(P_y)’ = \frac{P_y}{-P_z}$이다.
-
Z 좌표가 항상 -인 이유는 우리가 오른손 좌표계를 사용하고 있기 때문이다.
Affine matrix configuration
-
Affine matrix를 설명하기에 앞서, 이전 장에서 (x, y, z, 1)의 형태로 3D Point를 나타내준 다음에 Affine matrix와의 곱을 진행한다고 했는데, 이 때 이 1은 보통 w로 표시하고, 이렇게 나타낸 좌표들을 Homogeneous coordinate라고 표현한다.
-
즉, (x, y, z, w)로 표시하는게 Homogeneous coordinate인 것이다.
-
사실 이 좌표계는 $(\frac{x}{w}, \frac{y}{w}, \frac{z}{w}, \frac{w}{w})$로 표현하는게 정확하다.
-
그 이유는 w가 만약 1이 아닐 경우, 즉 w에 어떤 연산이 행해진 경우에는 동등한 비교를 위해서 Homogeneous coordinate로 나타냈다고 말하려면 w로 나눠줌으로써 행해진 Transform에 대해 역연산을 수행할 수 있는 것이기 때문이다.
-
위 식이 드디어 Affine matrix를 나타낸다.
-
초록색 부분은 Rotation 및 Scale을. 빨간색 부분은 Translation 부분을 나타낸다.
-
이 행렬로 인한 Transform은 Affine transform이라고 한다고 설명했는데, 이는 역시 Linear transformation이기 때문에 선형성이 유지된다.
-
이미 연거푸 설명했지만, 위 그림이 바로 이 Matrix를 통해서 Transformation을 하는 과정을 나타낸 그림이다.
-
행렬 곱 한번 해보면 알겠지만, 이 때 w는 항상 1로 유지된다.
-
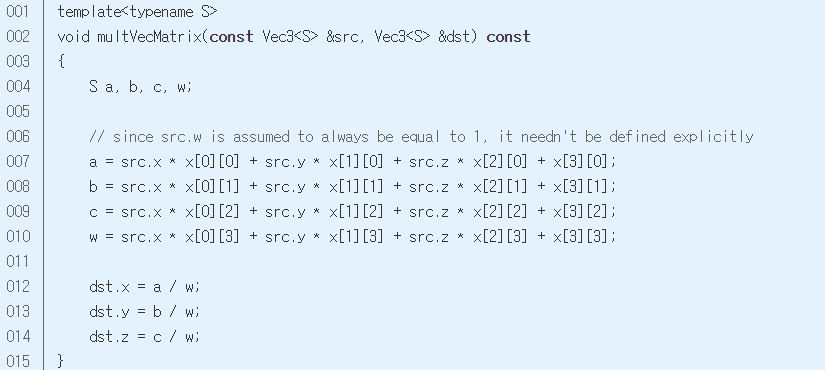
이를 코드로 나타내면 아래와 같다.
Projection matrix와 Affine matrix의 차이점
-
Affine matrix는 항상 $m_30, m_31, m_32, m_33$이 {0, 0, 0, 1}이지만, Projection matrix는 그렇지 않다.
-
따라서 Projection matrix와의 Transform을 수행하면 결과 W는 1이 아닐 수도 있다.
-
따라서 Projection matrix transform을 수행하면 결과값을 W로 나눠주는 과정이 필요하다.
-
따라서 코드는 아래와 같이 나타날 수 있다.
- 그렇지만 메트릭스 곱 할때마다 함수가 다르면 번거롭지? 합쳐놓은 버전이 있다~
-
또 Affine matrix는 그저 물체를 돌리거나 이동시키는 변환 이라는 것을 명심하고!
-
Projection matrix는 물체를 돌리거나 이동시키는 것 외에, NDC로 Projection 한다거나 하는걸 할 수 있는 Matrix라는 것을 기억해야한다.
-
이 Projection은 나머지 x, y, z 좌표들을 w로 나눈 다는 성질을 활용하여 w에 다른 값을 할당하는 것으로 모든 좌표들을 동등하게 변환시킨다.
-
즉, Affine transformation에다가 특정한 Transformation (공간적인!)을 한번 더 해준다고 보면 된다!
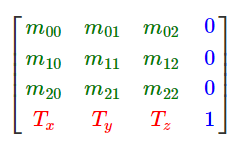
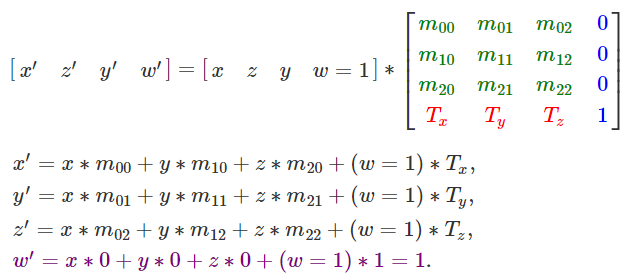




댓글남기기