[Graphics] The Perspective and Orthographic Projection Matrix
시작하기전에
-
이 글은 Scratchapixel 2.0의 글을 개인 공부 목적으로 번역 및 요약한 글입니다.
-
https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matrix-introduction
Projection matrix는 무엇인가?
-
이는 단지 $4x4 matrix$로 구성된다.
-
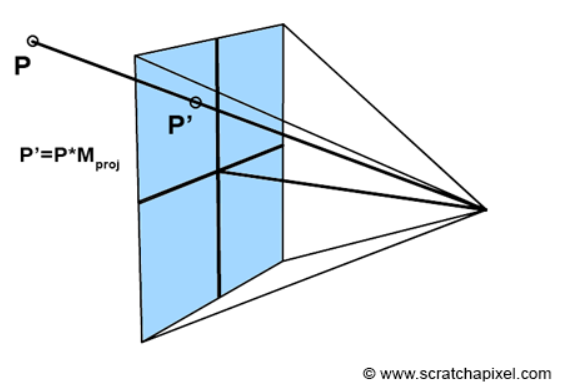
3D 좌표에 Projection matrix를 곱하면 새로운 2D 좌표가 나온다.
-
이는 3D 좌표에 Linear transfrom을 한다고 생각하면 된다.
-
Projection matrix는 여러가지가 있겠지만, 여기서 말하는 Projection matrix란 Computer graphics에서 화면에 Vertex를 표시하기 위해 정의한 공간 NDC(Normalized Device Coordinate)로 Projection 시키는 Matrix를 의미한다.
-
NDC는 Frustum(상, 하, 좌, 우, Near plane, Far plane으로 구성되는 육면체) 안에 좌표를 의미한다.
-
(첨언) 이 좌표계는 x, y 둘다 -1 ~ 1 사이의 값을 갖는데 이는 랜더링 할 화면의 해상도가 변하더라도 Normalized 되어 있기 때문에 변환이 빠르다는 장점을 가지고 있다.
Projection matrix 사용 코드 및 설명
- $Camera coordinate \to NDC coordinate$
- $M_proj$, 즉 Projection matrix는 아래와 같이 나타낼 수 있다.
-
위 코드에 나오는 near, t, b, l, r은 각각 Near plane, top, bottom, left, right를 의미한다.
-
이 메트릭스를 통해 우리는 화면 중심으로의 축 (Z축)으로의 분할 및 NDC 평면으로의 Mapping을 가능하게 한다.
Projection matrix의 특징
-
Projection matrix는 Vertex 혹은 3D Point를 변환하는데 사용한다. (벡터가 아니다.)
-
어 그런데 우리 Projection matrix는 4x4라고 했는데? 그럼 어떻게 3D Point와 연산을 하지?
-
이 때 우리는 마지막 Coordinate를 1로 둔다. (3D Point를 사용해 Projection 할 때만)
-
즉, (X, Y, Z, 1)의 형태가 되는 것이다.
-
이 변환을 우리는 Affine transformation이라고 한다. (In mathmatics)
Projection matrix가 왜 필요한가?
-
Camera 3D Point를 NDC로 변환하기 위해서!
-
옛날 GPU들은 Projection matrix를 직접 입력해줘야 했다고 한다. (아래가 옛날에 사용되었던 Projection matrix 코드) (이건 안봐도 될 듯)
-
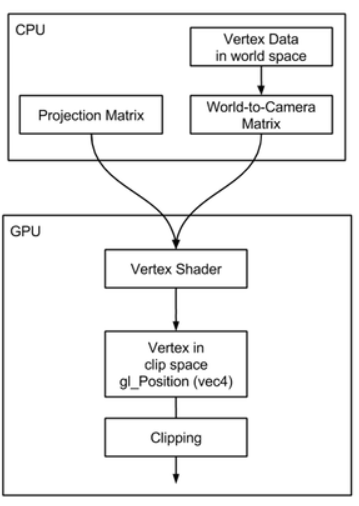
현재에는 Vertex shader에서 Projection matrix가 활용되는데, Normal point -> NDC가 아니라 Normal point -> clip space로 변환을 한다고 한다.
-
Clip space란, NDC로 가기 위한 중간 과정으로 보통은 Clip space = NDC라고 나타내는 것 같은데, 정확히는 Clip space는 Frustum에 의해 정의된 영역을 의미하는 것 같고, 그 다음에 Normalize 과정을 거치면 NDC로 Projection 되는 듯 하다.
-
아래는 Vertex shader를 이용해서 Clip space까지 변환하는 과정을 나타낸다.
- Projection matrix는 $Camera coordinate \to NDC$이다. World 좌표계가 아니다. 따라서 World 좌표계 * 카메라 좌표계 * Projection matrix의 순서로 곱해지는 것이 필요하다. 아래는 관련 코드이다.
-
참고로 월드 좌표계는 원점이 정해져 있지 않고, 따로 지정된 원점으로부터 좌표를 표시하는 좌표계를 의미한다.
-
카메라 좌표계는 카메라를 기준으로 나타나는 좌표계를 의미한다.
Perspective and Orthogonal projection matrix
-
Perspective든 Orthogonal이든 둘 다 목적은 역시 3D Point를 2D point로 Projection 하는 것이다.
-
Perspective는 말 그대로, 원근감을 사용하여 멀리 있을 수록 물체가 작아지는 표현 방식을 의미.
-
Orthogonal은 화각이 매우 작아지면 Frustum을 정의하는 4개의 선이 평행해지고, 그러면 거리라는게 의미가 없어지므로, 이 때 물체의 크기는 모두 똑같이 나타나게 된다는 표현 방식이다.
-
Orthogonal projection을 사용한 예시로는 Sim city가 있다.





댓글남기기