[Discussion] RELU가 sigmoid보다 더 많이 사용되는 이유는?

1 분 소요

Background

RelU나 Sigmoid는 activation function의 종류 중 하나이며, 입력 신호를 원하는 출력 신호의 형태로 변환시켜주기 위한 함수이다.
Relu 및 Sigmoid는 둘 다 비선형 함수의 형태를 띄고 있는데, 이는 네트워크를 깊게 디자인하기위해선 비선형함수가 필수적으로 여겨지기 때문이다.
그 이유는, 데이터가 매우 간단할 때에는 선형 함수로도 올바른 Decision boundary를 가질 수 있지만, 데이터의 차원이 늘어나고 분포가 다양해지면서 점차 선형 함수로는 올바르게 데이터를 나누기 힘들기 때문이다.
수학적으로 간단하게 말하자면, 선형 함수는 선형성을 만족시키기 때문에 다중 함수의 결합이 그저 a(b(c(d(e(x)))))와 같이 중첩되어 언제나 선형성을 만족하는 함수의 형태로 고정될 수 밖에 없지만, 비 선형 함수는 그런 제약에서 자유롭기 때문에 좀 더 데이터에 맞는 boundary를 잘 찾을 수 있기 때문이다.
Sigmoid
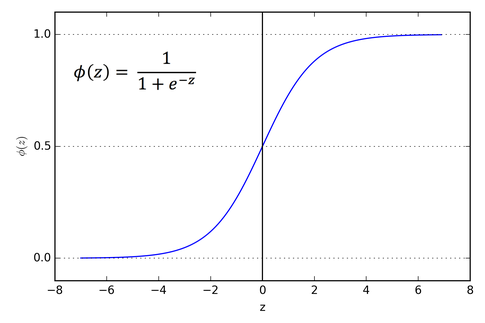
- Sigmoid 함수는 위와 같은 형태를 가지는 비선형함수이며, Input을 0과 1사이의 값으로 변환시켜준다.
- 보통 Binary cross-entropy와 결합되어 Binary classification task에 사용된다.
ReLU
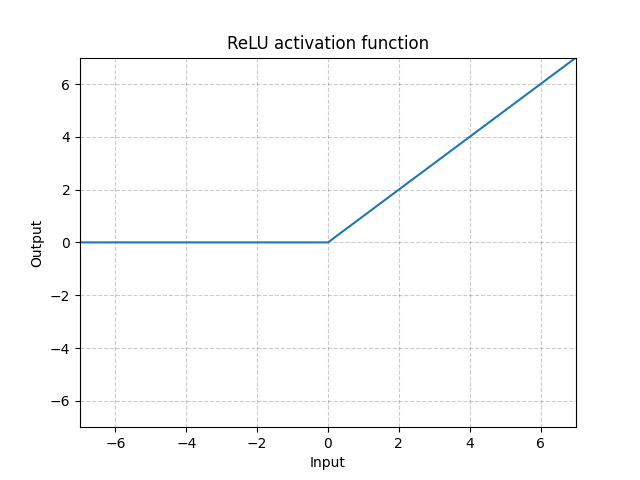
- ReLU 함수 역시 위와 같은 형태를 가지는 비선형함수이며, Input 중 0이상의 값만 남기는 함수입니다.
- 최근에는 범용적으로, Sigmoid 보다 더 많이 사용되는 함수입니다.

sigmoid보다 ReLU가 많이 사용되는 이유가 뭘까요?
가장 큰 이유는 바로 Gradient vanishing problem을 해결하기 위함입니다.
Gradient vanishing problem이란, backpropagation 단계에서 게속해서 미분을 취하기 때문에, 원래의 정보가 마지막 레이어까지 전파되지 못하여 학습이 골고루 되지 못하는 현상을 가리킵니다.
여기서, 만약 레이어마다 sigmoid를 사용한다면 어떻게 될까요?
sigmoid는 입력값을 0~1사이 값으로 만들기 때문에, 매 레이어를 거칠 때 마다 입력값은 기하급수적으로 줄어들게 됩니다.
반면에, ReLU 같은 경우에는, 입력의 양의 값을 그대로 보존하면서도 비 선형성을 가미할 수 있기 때문에, gradient vanishing problem으로 부터 자유로운 장점이 있기 때문에, sigmoid보다 ReLU를 많이 사용하는 것입니다.
때로는 Hidden layer에서는 LeLU를 사용하되, 맨 마지막 레이어만 sigmoid로 바꾸어, 최종 output은 0~1 사이의 형태로 가져가면서도 gradient vanishing problem을 해결하는 방법을 사용하기도 합니다.

RelU는 음의 입력값을 고려하지 못해 정보의 손실이 있으며, 극단적인 경우 입력이 모두 0 이하이면 학습이 불가능하다는 단점이 있다.
어? 이건 좀 다른 얘긴데 RelU의 그래프는 단순한 그래프니까 그 RelU의 결합 역시 단순한 그래프가 되지 않나?
- RelU의 그래프는 단순하지만, 그 단순한 그래프는 그대로 적용되는 것이 아닌 데이터에 적용된다는 점을 생각해야한다.
- 데이터에 RelU가 적용되면, 양의 값만 남을거고, 그건 연속적이지도 않은 그래프를 근사할 수도 있다.
- 따라서, 해당 그래프의 결합으로 구성된 그래프는 매우 유연하게 변할 수 있는 것이다.